牛客面试必刷101（包含经典排序算法）

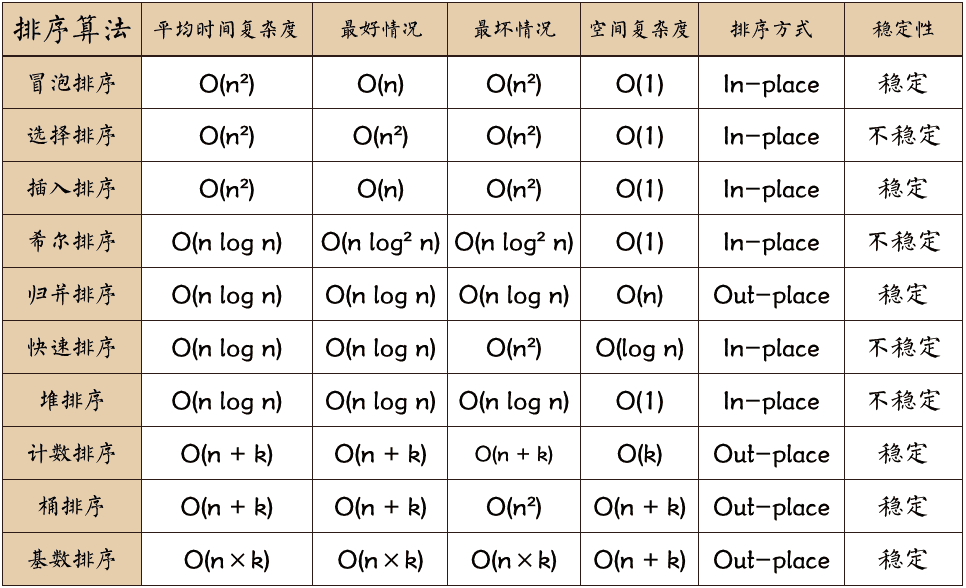
面试算法准备(Java)

十大经典排序算法

经典的十大排序算法可以大致分为两类：

1. 比较类排序：

• 冒泡排序 =》快速排序（冒泡排序优化）
• 插入排序=》希尔排序（插入排序优化）
• 选择排序=》堆排序（选择排序优化）
• 归并排序（二路、多路）

2. 非比较类排序：

• 计数排序 = 》桶排序

• 基数排序

冒泡排序

public class BubbleSort {
    public static void main(String[] args) {
        int[] ints = new int[]{2343, 234, 765, 1, 23, 5, 3, 2, 0, 3};
        bubbleSort(ints);
        for (int i : ints) {
            System.out.print(i + "\t");
        }
    }

/*    从第一个元素开始一个一个的比较相邻的元素，如果第一个比第二个大即a[1]>a[2]，就彼此交换。
    从第一对到最后一对，对每一对相邻元素做一样的操作。此时在最后的元素应该会是最大的数，我们也称呼一遍这样的操作为一趟冒泡排序。
    针对所有的元素重复以上的步骤，每一趟得到的最大值已放在最后，下一次操作则不需要将此最大值纳入计算。
    持续对每次对越来越少的元素，重复上面的步骤。
    直到所有的数字都比较完成符合a[i]<a[i+1]，即完成冒泡排序。*/
    

    /**
     * 冒泡排序
     * 空间复杂度:S(n) = O(1)
     * 时间复杂度:最坏O(n^2)，最好O(n)，平均O(n^2)
     * 稳定排序
     *
     * @param ints 无序数组
     */
    public static void bubbleSort(int[] ints) {
        for (int i = 0; i < ints.length - 1; i++) {
            boolean isChange = false;//优化，如果某一轮发现没有能交换的说明当前升序，无需继续遍历
            for (int j = 0; j < ints.length - 1 - i; j++) {
                if (ints[j] > ints[j + 1]) {
                    //交换，每轮循环把当前相较最大的放到最后
                    int swap = ints[j];
                    ints[j] = ints[j + 1];
                    ints[j + 1] = swap;//基本数据类型直接复制，而不是引用
                    isChange = true;
                }
            }
            if (!isChange) {
                break;
            }
        }
    }
}

快速排序

public class QuickSort {
    public static void main(String[] args) {
        int[] ints = new int[]{2343, 234, 765, 1, 23, 5, 3, 2, 0, 3};
        quickSort(ints, 0, ints.length - 1);
        for (int i : ints) {
            System.out.print(i + "\t");
        }
    }


/*    在数组中选择一个基准点
    分别从数组的两端扫描数组，设两个指示标志
    从后半部分开始，如果发现有元素比该基准点的值小，就交换位置
    然后从前半部分开始扫描，发现有元素大于基准点的值，继续交换位置
    如此往复循环，然后把基准点的值放到high这个位置,排序完成
    以后采用递归的方式分别对前半部分和后半部分排序，当前半部分和后半部分均有序时该数组就自然有序了。*/
    
    
    /**
     * 快速排序
     * 空间复杂度:S(n) = O(nlog2n)
     * 时间复杂度:最好O(nlogn) 最坏O(n^2) 平均O(nlogn)
     * 不稳定排序
     *
     * @param ints  数组
     * @param left  开始的左边下标
     * @param right 结束的右边下标
     */
    public static void quickSort(int[] ints, int left, int right) {
        //递归退出条件
        if (left >= right) {
            return;
        }
        int start = left;
        int end = right;
        //每次递归把第一个元素放到正确位置
        while (start < end) {
            //易错，一定要start<end，因为在循环里面出现等于的情况的时候就会发生越界的可能，并且如果以第一个数为基准就需要先比较后面的再比较前面的，反之
            //每轮把遍历到的位置左边都<=第一个元素，右边都>=第一个元素
            while (start < end && ints[end] >= ints[left]) {
                end--;
            }
            while (start < end && ints[start] <= ints[left]) {
                start++;
            }
            //前面while里面的start < end保证了最后start要么<end要么=end
            if (start == end) {
                int temp = ints[left];
                ints[left] = ints[end];
                ints[end] = temp;
            } else {
                int temp = ints[start];
                ints[start] = ints[end];
                ints[end] = temp;
            }
        }
        //最后start一定=end
        quickSort(ints, left, start - 1);
        quickSort(ints, start + 1, right);
    }
}

插入排序

public class InsertionSort {
    public static void main(String[] args) {
        int[] ints = new int[]{2343, 234, 765, 1, 23, 5, 3, 2, 0, 3};
        insertionSort(ints);
        for (int i : ints) {
            System.out.print(i + "\t");
        }
    }

/*    每次从无序表中取出第一个元素，把它插入到有序表的合适位置，使有序表仍然有序。
    第一趟比较前两个数，然后把第二个数按大小插入到有序表中；
    第二趟把第三个数据与前两个数从后向前扫描，把第三个数按大小插入到有序表中；
    依次进行下去，进行了(n-1)趟扫描以后就完成了整个排序过程。*/

    /**
     * 插入排序
     * 空间复杂度:S(n) = O(1)
     * 时间复杂度:最好情况O(n^2) 最坏情况O(n^2) 平均情况O(n^2)
     * 稳定排序
     *
     * @param ints 数组
     */
    public static void insertionSort(int[] ints) {
        //每次把当前遍历到的数放到正确的位置
        for (int i = 1; i < ints.length; i++) {
            int index = i;//最终value需要插入的正确的下标
            int value = ints[i];

            //个人更喜欢的思路，但while更简洁
            for (int j = i - 1; j >= 0; j--) {
                if (ints[j] > value) {
                    ints[j + 1] = ints[j];
                } else {
                    ints[j + 1] = value;
                    break;
                }
                //走到这里说明到最后一个都比需要归位的值大，如果有比他小的已经放到位置并且break
                if (j == 0) {
                    ints[j] = value;
                }
            }


            //往前比较直到发现比某个数小,否则就把比这个数大的数往后移动一位
            //按照后面希尔排序往前看，index>0可以写成index-1>=0
            while (index > 0 && ints[index - 1] > value) {
                ints[index] = ints[index - 1];
                index--;
            }
            //找到比需要归位的数字小的数字，就把需要归位的数字插在其后面一位
            ints[index] = value;
        }
    }
}

希尔排序

public class ShellSort {

    public static void main(String[] args) {
        int[] ints = new int[]{2343, 234, 765, 1, 23, 5, 3, 2, 0, 3};
        shellSort(ints);
        for (int i : ints) {
            System.out.print(i + "\t");
        }
    }

/*    选择一个增量序列 t1，t2，……，tk，其中 ti > tj, tk = 1；
    按增量序列个数 k，对序列进行 k 趟排序；
    每趟排序，根据对应的增量 ti，将待排序列分割成若干长度为 m 的子序列，分别对各子表进行直接插入排序。
    仅增量因子为 1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。*/
    
    /**
     * 希尔排序
     * 希尔排序是基于插入排序的，简单插入排序就是步长为1的希尔排序
     * 空间复杂度:S(n) = O(1)
     * 时间复杂度:最好情况:O(n) 最坏情况O(n^2) 平均情况O(n^2)
     * 不稳定排序
     *
     * @param ints 数组
     */
    public static void shellSort(int[] ints) {
        //步长，一般这样规定步长，决定进行多少次插入排序
        for (int i = ints.length / 2; i > 0; i /= 2) {
            //之后就是插入排序的模板
            for (int j = i; j < ints.length; j++) {
                //这里是j++，易错，每轮每个跳步中符合跳步的组合都进行排序，故j++
                int index = j;
                int value = ints[j];
                //index-i >= 0也就是防超界，前面的一个值跟需要插入正确的位置比，距离当前遍历到的数的步长为i的数字的下标>=0
                while (index - i >= 0 && ints[index - i] > value) {
                    ints[index] = ints[index - i];
                    index -= i;
                }
                ints[index] = value;
            }
        }
    }
}

选择排序

public class SelectSort {
    public static void main(String[] args) {
        int[] ints = new int[]{2343, 234, 765, 1, 23, 5, 3, 2, 0, 3};
        selectSort(ints);
        for (int i : ints) {
            System.out.print(i + "\t");
        }
    }

/*    首先设置两个记录i和j，i从数组第一个元素开始，j从(i+1)个元素开始。
    接着j遍历整个数组，选出整个数组最小的值，并让这个最小的值和i的位置交换。
    i选中下一个元素(i++)，重复进行每一趟选择排序。
    持续上述步骤，使得i到达(n-1)处，即完成排序 。*/
    
    /**
     * 选择排序
     * 空间复杂度:S(n) = O(1)
     * 时间复杂度:最好O(1) 最坏O(n^2) 平均O(n^2)
     * 不稳定排序
     *
     * @param ints 数组
     */
    public static void selectSort(int[] ints) {
        for (int i = ints.length - 1; i >= 0; i--) {
            int max_index = i;
            //每轮把最大的归位，从后往前遍历
            for (int j = i - 1; j >= 0; j--) {
                if (ints[j] > ints[max_index]) {
                    max_index = j;
                }
            }
            //当前的不是最大的
            if (max_index != i) {
                int temp = ints[i];
                ints[i] = ints[max_index];
                ints[max_index] = temp;
            }
        }

/*        for (int i = 0; i < ints.length; i++) {

            int min_index = i;

            //每轮把当前相对最小的归位
            for (int j = i + 1; j < ints.length; j++) {
                if (ints[j] < ints[min_index]) {
                    min_index = j;
                }
            }

            if (min_index != i) {
                //需要把最小的归位
                int temp = ints[i];
                ints[i] = ints[min_index];
                ints[min_index] = temp;
            }
        }*/
    }
}

堆排序

public class HeapSort {
    public static void main(String[] args) {
        int[] ints = new int[]{2343, 234, 765, 1, 23, 5, 3, 2, 0, 3};
        heapSort(ints);
        for (int i : ints) {
            System.out.print(i + "\t");
        }
    }

    /*堆是一种非线性的数据结构，其实就是利用完全二叉树的结构来维护的一维数组，利用这种结构可以快速访问到需要的值，堆可以分为大顶堆和小顶堆。
    大顶堆：每个结点的值都大于或等于其左右孩子结点的值
    小顶堆：每个结点的值都小于或等于其左右孩子结点的值*/

    /*首先把待排序的元素按照大小在二叉树位置上排列，且要满足堆的特性，如果根节点存放的是最大的数，则叫做大根堆，反之就叫做小根堆了。
    根据这个特性就可以把根节点拿出来，然后再堆化下，即用父节点和他的孩子节点进行比较，取最大的孩子节点和其进行交换，再把根节点拿出来，一直循环到最后一个节点，就排序好了。*/

    /**
     * 堆排序
     * 空间复杂度:S(n) = O(1)
     * 时间复杂度:最好O(n) 最坏O(n^2) 平均O(nlogn)
     * 不稳定排序
     *
     * @param ints 数组
     */
    public static void heapSort(int[] ints) {
        //建堆，一开始就把堆建好，后面递归就行，这里从ints.length / 2 - 1开始是因为在下面都是叶子节点了
        for (int i = ints.length / 2 - 1; i >= 0; i--) {
            heapSortStart(ints, ints.length, i);
        }
        //排序
        for (int i = ints.length - 1; i >= 0; i--) {
            swap(ints, i, 0);//第一次已经完成建堆，交换最后一个和第一个，相当于最大的交换到最后，第一次建堆最大的在0下标
            heapSortStart(ints, i, 0);//易错，注意长度发生了变化
        }
    }

    /**
     * 堆排序虽然是要维护堆，但是以象征来看确实是堆，但原本还是一个数组
     *
     * @param ints   数组
     * @param length 需要维护的数组长度
     * @param i      维护的目标节点位置，当前维护的父节点的位置
     */
    public static void heapSortStart(int[] ints, int length, int i) {
        //要把最大的数值放到父节点
        int largest = i;
        int lson = i * 2 + 1, rson = i * 2 + 2;//树对应一维数组的下标
        if (lson < length && ints[lson] > ints[largest]) {
            largest = lson;
        }
        if (rson < length && ints[rson] > ints[largest]) {
            largest = rson;
        }
        if (largest != i) {
            swap(ints, largest, i);//把最大的交换到i位置并维护交换后的位置的堆
            heapSortStart(ints, length, largest);
        }
    }

    /**
     * @param ints  数组
     * @param left  要交换位置的第一个数的下标
     * @param right 要交换位置的第二个数的下标
     */
    public static void swap(int[] ints, int left, int right) {
        int temp = ints[left];
        ints[left] = ints[right];
        ints[right] = temp;
    }
}

归并排序

public class MergeSort {
    public static void main(String[] args) {
        int[] ints = new int[]{2343, 234, 765, 1, 23, 5, 3, 2, 0, 3};
        mergeSort(ints, 0, ints.length - 1);
        for (int i : ints) {
            System.out.print(i + "\t");
        }
    }


/*    申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
    设定两个指针，最初位置分别为两个已经排序序列的起始位置
    比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
            重复步骤c直到某一指针超出序列尾
    将另一序列剩下的所有元素直接复制到合并序列尾*/

    /**
     * 归并排序
     * 这里先进行划分，之后进行归并
     * 空间复杂度:S(n)=O(n)
     * 时间复杂度:最好O(nlogn) 最好O(nlogn) 平均O(nlogn)
     * 稳定排序
     *
     * @param ints  需要排序的原本数组
     * @param left  开始排序的最左边的下标
     * @param right 开始排序的最右边的下标
     */
    public static void mergeSort(int[] ints, int left, int right) {
        //进行划分
        //只有一个数字就没必要划分了
        if (left < right) {
            //这样划分其实就是不断分成很多子集进行处理，最小的就是只剩两个数字进行比较
            int mid = (left + right) / 2;
            mergeSort(ints, left, mid);
            mergeSort(ints, mid + 1, right);
            //进行归并，两个相对有序的数组进行合并
            merge(ints, left, mid, right, new int[ints.length]);
        }
    }

    /**
     * 归并过程，合并两个相对有序的数组
     *
     * @param ints  需要排序的原本数组
     * @param left  开始排序的最左边的下标
     * @param mid   排序段的中间坐标
     * @param right 开始排序的最右边的下标
     * @param temp  临时数组
     */
    public static void merge(int[] ints, int left, int mid, int right, int[] temp) {
        int left_start = left;
        int right_start = mid + 1;
        int index = 0;//即将要放入temp数组的位置下标，也就是temp的长度
        //两边进行比较，较小的放入temp数组并进行移动，之后进行下一轮比较
        while (left_start <= mid && right_start <= right) {
            if (ints[left_start] <= ints[right_start]) {
                temp[index++] = ints[left_start++];
            } else {
                temp[index++] = ints[right_start++];
            }
        }
        //左边还有没比较完的
        while (left_start <= mid) {
            temp[index++] = ints[left_start++];
        }
        //右边还有没比较完的
        while (right_start <= right) {
            temp[index++] = ints[right_start++];
        }
        //放回原本的数组，进行复制
        for (int i = 0; i < index; i++) {
            ints[left++] = temp[i];//易错，注意是从开始进行排序的位置进行原本数组的赋值
        }
    }
}

计数排序

public class CountingSort {
    public static void main(String[] args) {
        int[] ints = new int[]{2343, 234, 765, 1, 23, 5, 3, 2, 0, 3};
        countingSort(ints);
        for (int i : ints) {
            System.out.print(i + "\t");
        }
    }

/*    找出待排序的数组中最大和最小的元素
    统计数组中每个值为i的元素出现的次数，存入数组C的第i项
    对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）
    反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1*/
    
    /**
     * 计数排序
     * 缺点很明显，就是不能处理小数
     * 空间复杂度S(n) = O(n+k)
     * 时间复杂度:最好O(n+k) 最坏O(n+k) 平均O(n+k)
     * 稳定排序
     *
     * @param ints 数组
     */
    public static void countingSort(int[] ints) {
        if (ints == null || ints.length == 0) {
            return;
        }
        //得到最大值
        int max = ints[0];
        for (int i = 1; i < ints.length; i++) {
            if (ints[i] > max) {
                max = ints[i];
            }
        }
        //新建一个长度为max+1的数组，最后一个的下标要为max
        int[] temp = new int[max + 1];
        for (int i : ints) {
            temp[i]++;
        }
        //按照下标统计temp数组中元素的值，就知道原本数组中有多少个当前下标的值，直接填入即可
        int t = 0;
        for (int i = 0; i < temp.length; i++) {
            if (temp[i] != 0) {
                for (int j = 0; j < temp[i]; j++) {
                    ints[t++] = i;
                }
            }
        }
    }
}

桶排序

public class BucketSort {
    public static void main(String[] args) {
        int[] ints = new int[]{2343, 234, 765, 1, 23, 5, 3, 2, 0, 3};
        bucketSort(ints);
        for (int i : ints) {
            System.out.print(i + "\t");
        }
    }
    
    /**
     * 桶排序
     * 在计数排序的基础上来的，有个思路就行，里面还用了其他排序
     * 就是按照不同的范围分成多个桶，不同的数放到不同范围的桶内，桶内进行排序然后拼接起来即可
     * 空间复杂度:S(n) = O(n+k)
     * 时间复杂度:最好O(n+k) 最坏O(n^2) 平均O(n+k)
     * 稳定排序
     *
     * @param ints 数组
     */
    public static void bucketSort(int[] ints) {
        if (ints == null || ints.length == 1) {
            return;
        }
        int min = ints[0];
        int max = ints[0];
        //找出最大和最小值
        for (int i = 1; i < ints.length; i++) {
            if (ints[i] > max) {
                max = ints[i];
            }
            if (ints[i] < min) {
                min = ints[i];
            }
        }
        //分桶
        int buketNum = (max - min) / ints.length + 1;
        //借助list去完成存储
        ArrayList<ArrayList<Integer>> bucketList = new ArrayList<>(buketNum);
        for (int i = 0; i < buketNum; i++) {
            bucketList.add(new ArrayList<>());
        }
        //往桶中填充数据
        for (int i : ints) {
            bucketList.get((i - min) / ints.length).add(i);//相同商的也就是满足范围放到桶中
        }
        //每个桶内数据自动进行排序，这里就需要使用其他排序函数，这里用api了，可以用快排、选择排序。。。
        for (int i = 0; i < buketNum; i++) {
            Collections.sort(bucketList.get(i));
        }
        //统计桶中数据
        int t = 0;
        for (int i = 0; i < buketNum; i++) {
            ArrayList<Integer> list = bucketList.get(i);
            for (Integer integer : list) {
                ints[t++] = integer;
            }
        }
    }
}

基数排序

public class RadixSort {
    public static void main(String[] args) {
        int[] ints = new int[]{2343, 234, 765, 1, 23, 5, 3, 2, 0, 3};
        radixSort(ints);
        for (int i : ints) {
            System.out.print(i + "\t");
        }
    }

    /* 假设存在一个序列{50, 123, 543, 187, 49, 30, 0, 2, 11, 100}
    任何一个阿拉伯数，它的各个位数上的基数都是以0~9来表示的。所以我们不妨把0~9视为10个桶。
    我们先根据序列的个位数的数字来进行分类，将其分到指定的桶中。
    分类后，我们在从各个桶中，将这些数按照从编号0到编号9的顺序依次将所有数取出来。
    得到的序列就是个位数上呈递增趋势的序列。
    按照上图个位数排序：{50, 30, 0, 100, 11, 2, 123, 543, 187, 49}。
    接下来对十位数、百位数也按照这种方法进行排序，最后就能得到排序完成的序列。*/

    /**
     * 基数排序
     * 按照数位，个位到十位到百位。。。进行桶排序
     * 空间复杂度:S(n) = O(n+k)
     * 时间复杂度:最好O(n*k) 最坏O(n*k) 平均O(n*k)
     * 稳定排序
     *
     * @param ints 数组
     */
    public static void radixSort(int[] ints) {
        if (ints == null || ints.length == 1) {
            return;
        }
        int[][] save = new int[10][ints.length];//保存具体的值的临时数组
        int[] bucket_num = new int[10];//保存每个桶中现在的数字个数
        //寻找最大的数字，确定最大的数字的长度
        int max = ints[0];
        for (int i = 1; i < ints.length; i++) {
            if (ints[i] > max) {
                max = ints.length;
            }
        }
        //控制进行数位桶排序的次数
        for (int i = 0; i < (max + "").length(); i++) {
            //控制进行排序遍历的顺序
            //把数放到桶中
            for (int j = 0; j < ints.length; j++) {
                int temp = ints[j] / (int) Math.pow(10, i) % 10;
                save[temp][bucket_num[temp]++] = ints[j];
            }
            //将数从桶中读出放回原数组
            int t = 0;
            for (int j = 0; j < bucket_num.length; j++) {
                if (bucket_num[j] != 0) {
                    for (int k = 0; k < bucket_num[j]; k++) {
                        ints[t++] = save[j][k];
                    }
                }
                //还原bucket_num，把每个桶内保存的内容清空
                bucket_num[j] = 0;
            }
        }
    }
}

题目练手链接

• LCR 159. 库存管理 III

LCR 159. 库存管理 III - 力扣（LeetCode）

class Solution {
    public int[] inventoryManagement(int[] stock, int cnt) {
        // 这就是考排序了，不用内置函数
        int[] temp = new int[stock.length];

        // 1.归并排序
        // mergeSort(stock,temp,0,stock.length-1);

        // 2.冒泡排序
        // bubbleSort(stock);

        // 3.选择排序
        // selectSort(stock);

        // 4.快速排序
        // quickSort(stock, 0, stock.length - 1);

        // 5.堆排序
        heapSort(stock);

        int[] result = new int[cnt];
        for (int i = 0; i < cnt; i++) {
            result[i] = stock[i];
        }
        return result;
    }

    // 1.归并排序
    public void mergeSort(int[] stock, int[] temp, int start, int end) {
        if (start < end) {
            int mid = start + (end - start) / 2;
            // 处理好左右
            mergeSort(stock, temp, start, mid);
            mergeSort(stock, temp, mid + 1, end);
            // 合并两个排好序的片段
            merge(stock, temp, start, mid, end);
        }
    }

    public void merge(int[] stock, int[] temp, int start, int mid, int end) {
        int left = start, right = mid + 1, t = start;
        // 哪个小哪个先放进去
        while (left <= mid && right <= end) {
            if (stock[left] <= stock[right]) {
                temp[t++] = stock[left++];
            } else {
                temp[t++] = stock[right++];
            }
        }
        while (left <= mid) {
            temp[t++] = stock[left++];
        }
        while (right <= end) {
            temp[t++] = stock[right++];
        }
        // 贴回原数组
        for (int i = start; i <= end; i++) {
            stock[i] = temp[i];
        }
    }

    // 2.冒泡排序
    public void bubbleSort(int[] stock) {
        // 每轮将最大的复位
        // 优化，看本轮是否能交换，不能就说明是升序
        boolean flag = true;
        for (int i = 1; i < stock.length; i++) {
            if (flag) {
                boolean temp = false;
                // 交换
                for (int j = 1; j <= stock.length - i; j++) {
                    if (stock[j - 1] > stock[j]) {
                        // 交换
                        temp = true;
                        int change = stock[j - 1];
                        stock[j - 1] = stock[j];
                        stock[j] = change;
                    }
                }
                flag = temp;
            }
        }
    }

    // 3.选择排序
    public void selectSort(int[] stock) {
        for (int i = 1; i < stock.length; i++) {
            // 保存下标
            int max = 0;
            for (int j = 1; j <= stock.length - i; j++) {
                if (stock[j] > stock[max]) {
                    max = j;
                }
            }
            // 交换位置
            int temp = stock[max];
            stock[max] = stock[stock.length - i];
            stock[stock.length - i] = temp;
        }
    }

    // 4.快速排序
    public void quickSort(int[] stock, int start, int end) {
        if (start >= end) {
            return;
        }
        int left = start, right = end;
        while (left < right) {
            // 每轮都将小于等于基准元素的放在左边，大于等于基准元素的放在右边，先移动右指针
            while (left < right && stock[right] >= stock[start]) {
                right--;
            }
            while (left < right && stock[left] <= stock[start]) {
                // 必须等于,才能继续往右边走，不然就一直定在第一个位置了
                left++;
            }
            // 到这里说明找到左边比基准元素大，右边比基准元素小的
            if (left < right) {
                int temp = stock[left];
                stock[left] = stock[right];
                stock[right] = temp;
            }
        }
        // 交换基准元素
        int temp = stock[start];
        stock[start] = stock[left];
        stock[left] = temp;
        // 递归处理完成的元素的左右
        quickSort(stock, start, left);
        quickSort(stock, left + 1, end);
    }

    // 5.堆排序
    public void heapSort(int[] stock) {
        // 堆排序的抽象的树结构（大顶堆）是满足父节点比孩子节点大就可以了；（小顶堆就反过来）
        // 一开始拿到数组需要先将无序的调整顺序建成一个大顶堆，之后将最大的放到最后的位置并重新维护堆就可以了
        // 从倒数第二层开始建堆（从有孩子节点开始），一直往上到父节点去建堆
        for (int i = stock.length / 2 - 1; i >= 0; i--) {
            heapify(stock, stock.length, i);
        }
        // 现在就是一个大顶堆里，下面就要交换顶的位置到最后一个，然后重新维护
        for (int i = stock.length - 1; i > 0; i--) {
            int temp = stock[0];
            stock[0] = stock[i];
            stock[i] = temp;
            // 之后重新维护堆，注意这时候长度要忽略最后一个位置，那长度刚好是i
            heapify(stock, i, 0);
        }
    }

    public void heapify(int[] stock, int n, int i) {
        // 维护某个节点的堆性质
        // 首先确认最大值的位置,确认左右节点的位置
        int largest = i, left = 2 * i + 1, right = 2 * i + 2;
        if (left < n && stock[left] > stock[largest]) {
            largest = left;
        }
        if (right < n && stock[right] > stock[largest]) {
            largest = right;
        }
        if (largest != i) {
            // 交换位置
            int temp = stock[largest];
            stock[largest] = stock[i];
            stock[i] = temp;
            // 交换位置后可能破坏堆性质需要递归处理一下,i被交换到了largest，直到处理进入的时候都i到正确位置
            heapify(stock, n, largest);
        }
    }
}

牛客网面试必刷Top101

链表

• BM1 反转链表
• BM2 链表内指定区间反转
• BM4 合并两个排序的链表
• BM5 合并k个已排序的链表
• BM6 判断链表中是否有环
• BM7 链表中环的入口结点
• BM8 链表中倒数最后k个结点
• BM10 两个链表的第一个公共结点
• BM11 链表相加(二)
• BM12 单链表的排序
• BM13 判断一个链表是否为回文结构
• BM14 链表的奇偶重排
• BM15 删除有序链表中重复的元素-I
• BM16 删除有序链表中重复的元素-II

BM1 反转链表

import java.util.*;

/*
 * public class ListNode {
 *   int val;
 *   ListNode next = null;
 *   public ListNode(int val) {
 *     this.val = val;
 *   }
 * }
 */

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param head ListNode类
     * @return ListNode类
     */
    public ListNode ReverseList (ListNode head) {
        ListNode lastNode = null;
        while (head != null) {
            ListNode temp =
                head.next;//保存当前节点的下一个，这样在修改当前节点的next指针后还能将下一个复制给当前对象进行遍历
            head.next =
                lastNode;//当前的next就是上轮的结果，每次都还需要保存上轮的访问的节点，并且一开始为空
            lastNode = head;
            head = temp;
        }
        return lastNode;
    }
}

BM2 链表内指定区间反转

懵逼，细看

时间复杂度O(n)，空间复杂度O(1)，一次遍历

import java.util.*;

/*
 * public class ListNode {
 *   int val;
 *   ListNode next = null;
 *   public ListNode(int val) {
 *     this.val = val;
 *   }
 * }
 */

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param head ListNode类
     * @param m int整型
     * @param n int整型
     * @return ListNode类
     */
    public ListNode reverseBetween (ListNode head, int m, int n) {
        //加个表头
        ListNode start = new ListNode(-1);
        start.next = head;
        //前序节点
        ListNode last = start;
        //当前节点
        ListNode cur = head;
        //找到m
        for (int i = 1; i < m; i++) {
            last = cur;
            cur = cur.next;
        }
        //从m反转到n
        for (int i = m; i < n; i++) {
            ListNode temp = cur.next;//先保存原本这个节点的next再更改
            cur.next =
                temp.next;//不断更改cur的下一个，直到到达n，这样最后会接到一起
            temp.next = last.next;//原本节点的next为last
            last.next =
                temp;//last是保存上一个，cur.next = temp.next那么last.next = temp
        }
        return start.next;
    }
}

BM4 合并两个排序的链表

import java.util.*;

/*
 * public class ListNode {
 *   int val;
 *   ListNode next = null;
 *   public ListNode(int val) {
 *     this.val = val;
 *   }
 * }
 */

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param pHead1 ListNode类 
     * @param pHead2 ListNode类 
     * @return ListNode类
     */
    public ListNode Merge (ListNode pHead1, ListNode pHead2) {
        ListNode result = null,first = pHead1,second = pHead2,tmp = null,last = null;
        while(first!=null&&second!=null){
            if(first.val<second.val){
                tmp = first;
                first = first.next;
            }else{
                tmp = second;
                second = second.next;
            }
            ListNode newNode = new ListNode(tmp.val);
            if(result==null){
                result = newNode;
                last = result;
            }else{
                last.next = newNode;
                last = last.next;
            }
        }
        while(first!=null){
            ListNode newNode = new ListNode(first.val);    
            if(result==null){
                result = newNode;
                last = result;
            }else{
                last.next = newNode;
                last = last.next;
            }
            first = first.next;
        }
        while(second!=null){
            ListNode newNode = new ListNode(second.val);    
            if(result==null){
                result = newNode;
                last = result;
            }else{
                last.next = newNode;
                last = last.next;
            }
            second = second.next;
        }
        return result;
    }
}

递归实现

/*
public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}*/
public class Solution {
    public ListNode Merge(ListNode list1,ListNode list2) {
        if(list1==null){
            return list2;
        }
        else if(list2==null){
            return list1;
        }
        if(list2.val>list1.val){
            list1.next = Merge(list1.next,list2);
            return list1;
        }
        else{
            list2.next = Merge(list1,list2.next);
            return list2;
        }
    }
}

BM5 合并k个已排序的链表

时间复杂度要为O(nlogn)

```



<a id="BM6 判断链表中是否有环"></a>

**BM6 判断链表中是否有环**

快慢指针，如果有环会碰到一起

```java
import java.util.*;
/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public boolean hasCycle(ListNode head) {
        ListNode fast = head;
        ListNode slow = head;
        while (fast != null && fast.next != null) {
            fast = fast.next.next;
            slow = slow.next;
            if (fast == slow) {
                return true;
            }
        }
        return false;
    }
}

BM7 链表中环的入口结点

空间复杂度 O(1)，时间复杂度 O(n)

据题干，不说别的，我们能发现这道题需要完成两个任务：

• 判断链表是否有环。（这个前面有）
• 在有环的链表中找到环的入口。

具体做法：（证明不看了，从链表头经过环入口到达相遇地方经过的距离等于整数倍环的大小，那我们从头开始遍历到相遇位置，和从相遇位置开始在环中遍历，会使用相同的步数，而双方最后都会经过入口到相遇位置这y个节点）

step 1：使用BM6.判断链表中是否有环中的方法判断链表是否有环，并找到相遇的节点。
step 2：慢指针继续在相遇节点，快指针回到链表头，两个指针同步逐个元素逐个元素开始遍历链表。
step 3：再次相遇的地方就是环的入口。

import java.util.*;
/*
 public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}
*/
public class Solution {

    public ListNode EntryNodeOfLoop(ListNode pHead) {
        //寻找是否有环
        ListNode fast = pHead, slow = pHead, slow_real = null;
        while (fast != null && fast.next != null) {
            fast = fast.next.next;
            slow = slow.next;
            if (fast == slow) {
                slow_real = slow;//相交点
                break;
            }
        }
        if (slow_real == null) {
            return null;//没有环
        }
        //寻找进入环东第一个节点
        fast = pHead;
        while (fast != slow_real) {
            fast = fast.next;
            slow_real = slow_real.next;
        }
        return slow_real;
    }
}

BM8 链表中倒数最后k个结点

最简单的思路就是借助栈，但是空间复杂度为O(n)

import java.util.*;

/*
 * public class ListNode {
 *   int val;
 *   ListNode next = null;
 *   public ListNode(int val) {
 *     this.val = val;
 *   }
 * }
 */

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param pHead ListNode类
     * @param k int整型
     * @return ListNode类
     */
    public ListNode FindKthToTail (ListNode pHead, int k) {
        List<ListNode>list = new ArrayList<>();
        ListNode tmp = pHead;
        while(tmp!=null){
            list.add(tmp);
            tmp = tmp.next;
        }
        if(list.size()<k||k==0){
            return null;
        }else{
            return list.get(list.size()-k);
        }
    }
}

还有简单的思路就是先遍历一遍到最后，这样就知道链表的长度，这样就可以再遍历一次看遍历多少个节点就找到正确的节点了

进阶思路为空间复杂度为O(1)，快慢指针，学习这种思路

（双指针指的是在遍历对象的过程中，不是普通的使用单个指针进行访问，而是使用两个指针（特殊情况甚至可以多个），两个指针或是同方向访问两个链表、或是同方向访问一个链表（快慢指针）、或是相反方向扫描（对撞指针），从而达到我们需要的目的。）

import java.util.*;

/*
 * public class ListNode {
 *   int val;
 *   ListNode next = null;
 *   public ListNode(int val) {
 *     this.val = val;
 *   }
 * }
 */

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param pHead ListNode类
     * @param k int整型
     * @return ListNode类
     */
    public ListNode FindKthToTail (ListNode pHead, int k) {
        //快慢指针
        ListNode slow = pHead;
        ListNode fast = pHead;
        //快指针先移动k步
        for (int i = 0; i < k; i++) {
            if (fast != null) {
                fast = fast.next;
            } else {
                //说明链表过短
                return null;
            }
        }
        //之后保持着fast比slow快k步的方式移动
        while (fast != null) {
            fast = fast.next;
            slow = slow.next;
        }
        return slow;
    }
}

BM10 两个链表的第一个公共结点

要求空间复杂度为O(1)

使用两个指针N1,N2，一个从链表1的头节点开始遍历，我们记为N1，一个从链表2的头节点开始遍历，我们记为N2。

让N1和N2一起遍历，当N1先走完链表1的尽头（为null）的时候，则从链表2的头节点继续遍历，同样，如果N2先走完了链表2的尽头，则从链表1的头节点继续遍历，也就是说，N1和N2都会遍历链表1和链表2。

因为两个指针，同样的速度，走完同样长度（链表1+链表2），不管两条链表有无相同节点，都能够到达同时到达终点。

（N1最后肯定能到达链表2的终点，N2肯定能到达链表1的终点）。

所以，如何得到公共节点：

有公共节点的时候，N1和N2必会相遇，因为长度一样嘛，速度也一定，必会走到相同的地方的，所以当两者相等的时候，则会第一个公共的节点
无公共节点的时候，此时N1和N2则都会走到终点，那么他们此时都是null，所以也算是相等了。

import java.util.*;
/*
public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}*/
public class Solution {
    public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {
        ListNode t1 = pHead1, t2 = pHead2;
        while (t1 != t2) {
            t1 = (t1 == null) ? pHead2 : t1.next;
            t2 = (t2 == null) ? pHead1 : t2.next;
        }
        return t1;
    }
}

BM11 链表相加(二)

step 1：任意一个链表为空，返回另一个链表就行了，因为链表为空相当于0，0加任何数为0，包括另一个加数为0的情况。
step 2：相继反转两个待相加的链表，反转过程可以参考反转链表。
step 3：设置返回链表的链表头，设置进位carry=0.
step 4：从头开始遍历两个链表，直到两个链表节点都为空且carry也不为1. 每次取出不为空的链表节点值，为空就设置为0，将两个数字与carry相加，然后查看是否进位，将进位后的结果（对10取模）加入新的链表节点，连接在返回链表后面，并继续往后遍历。
step 5：返回前将结果链表再反转回来。

import java.util.*;

/*
 * public class ListNode {
 *   int val;
 *   ListNode next = null;
 *   public ListNode(int val) {
 *     this.val = val;
 *   }
 * }
 */

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param head1 ListNode类
     * @param head2 ListNode类
     * @return ListNode类
     */
    public ListNode addInList (ListNode head1, ListNode head2) {
        //任何一个链表为空就返回另外一个
        if(head1==null){
            return head2;
        }
        if(head2==null){
            return head1;
        }
        //翻转完成
        head1 = reverseList(head1);
        head2 = reverseList(head2);
        //进行正常的计算，链表取巧就是加一个表头
        ListNode start = new ListNode(-1);
        ListNode head = start;
        int carry = 0;//进位符号
        //只要某个链表还有或者进位还有
        while (head1 != null || head2 != null || carry != 0) {
            int val1, val2;
            if (head1 == null) {
                val1 = 0;
            } else {
                val1 = head1.val;
            }
            if (head2 == null) {
                val2 = 0;
            } else {
                val2 = head2.val;
            }
            //插入新链表
            head.next = new ListNode((val1 + val2 + carry) % 10);
            head = head.next;
            carry = (val1 + val2 + carry) / 10; //更新进位
            //head1和head2移动到下一个
            if (head1 != null) {
                head1 = head1.next;
            }
            if (head2 != null) {
                head2 = head2.next;
            }
        }
        return reverseList(start.next);
    }

    //按照常规的加法计算就需要先翻转链表，翻转链表前面有
    public ListNode reverseList(ListNode head) {
        if (head == null) {
            return null;
        }
        ListNode cur = head;
        ListNode last = null;
        while (cur != null) {
            ListNode temp = cur.next;
            cur.next = last;
            last = cur;
            cur = temp;
        }
        return last;
    }
}

BM12 单链表的排序

简单的思路就是遍历单链表转换成数组进行排序，这里学基于链表的归并排序

step 1：首先判断链表为空或者只有一个元素，直接就是有序的。
step 2：准备三个指针，快指针right每次走两步，慢指针mid每次走一步，前序指针left每次跟在mid前一个位置。三个指针遍历链表，当快指针到达链表尾部的时候，慢指针mid刚好走了链表的一半，正好是中间位置。
step 3：从left位置将链表断开，刚好分成两个子问题开始递归。
step 4：将子问题得到的链表合并，参考合并两个有序链表。

import java.util.*;

/*
 * public class ListNode {
 *   int val;
 *   ListNode next = null;
 *   public ListNode(int val) {
 *     this.val = val;
 *   }
 * }
 */

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param head ListNode类 the head node
     * @return ListNode类
     */
    public ListNode sortInList (ListNode head) {
        // 分治，归并排序
        if (head == null || head.next == null) {
            return head;
        }
        ListNode left = head, mid = head.next, right = head.next.next;
        //右边指针到达末尾的时候,中间的指针指向该段链表的中间
        while (right != null && right.next != null) {
            left = left.next;
            mid = mid.next;
            right = right.next.next;
        }
        //左指针指向左段的左右一个节点，从这里断开
        left.next = null;
        //分成两段，合并排序好的两段
        return merge(sortInList(head), sortInList(mid));
    }

    //两个有序链表的合并
    public ListNode merge(ListNode head1, ListNode head2) {
        //其中一个为空就返回另外一个
        if (head1 == null) {
            return head2;
        }
        if (head2 == null) {
            return head1;
        }
        //经典加一个表头
        ListNode start = new ListNode(-1);
        ListNode cur = start;
        //两个链表都不为空
        while (head1 != null && head2 != null) {
            if (head1.val <= head2.val) {
                cur.next = head1;
                head1 = head1.next;
            } else {
                cur.next = head2;
                head2 = head2.next;
            }
            cur = cur.next;
        }
        //哪个链表还有内容就直接接到后面
        if (head1 != null) {
            cur.next = head1;
        }
        if (head2 != null) {
            cur.next = head2;
        }
        //返回值去掉表头
        return  start.next;
    }
}

BM13 判断一个链表是否为回文结构

借助List实现很容易，就先遍历链表然后将链表的所有值都放到List中，然后双指针对碰即可，如果在碰撞之前某个值不一样就返回fasle即可

学习双指针找中点的方法，空间复杂度为O(1)，快慢指针

我们首先来看看中点的特征，一个链表的中点，距离链表开头是一半的长度，距离链表结尾也是一半的长度，那如果从链表首遍历到链表中点位置，另一个每次遍历两个节点的指针是不是就到了链表尾，那这时候我们的快慢双指针就登场了：

具体做法：

step 1：慢指针每次走一个节点，快指针每次走两个节点，快指针到达链表尾的时候，慢指针刚好到了链表中点。
step 2：从中点的位置，开始往后将后半段链表反转。
step 3：按照方法三的思路，左右双指针，左指针从链表头往后遍历，右指针从链表尾往反转后的前遍历，依次比较遇到的值。

import java.util.*;

/*
 * public class ListNode {
 *   int val;
 *   ListNode next = null;
 *   public ListNode(int val) {
 *     this.val = val;
 *   }
 * }
 */

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param head ListNode类 the head
     * @return bool布尔型
     */
    public boolean isPail (ListNode head) {
        //空链表为回文
        if (head == null) {
            return true;
        }
        //快慢指针
        ListNode slow = head, fast = head;
        //快指针移动两步，慢指针移动一步
        while (fast != null && fast.next != null) {
            fast = fast.next.next;
            slow = slow.next;
        }
        //找到中点位置,从中点处，也就是慢指针处开始翻转后面的元素，快指针回到开头进行遍历，看是否是回文，翻转其实就是第一题
        ListNode start = slow, last = null;
        while (start != null) {
            ListNode tmp = start.next;
            start.next = last;
            last = start;
            start = tmp;
        }
        slow = last;
        //翻转后slow指针继续遍历
        fast = head;
        while (slow != null) {
            if (slow.val != fast.val) {
                return false;
            }
            slow = slow.next;
            fast = fast.next;
        }
        return true;
    }
}

BM14 链表的奇偶重排

空间复杂度O(1)，时间复杂度O(n)

step 1：判断空链表的情况，如果链表为空，不用重排。
step 2：使用双指针odd和even分别遍历奇数节点和偶数节点，并给偶数节点链表一个头。
step 3：上述过程，每次遍历两个节点，且even在后面，因此每轮循环用even检查后两个元素是否为NULL，如果不为再进入循环进行上述连接过程。
step 4：将偶数节点头接在奇数最后一个节点后，再返回头部。

import java.util.*;

/*
 * public class ListNode {
 *   int val;
 *   ListNode next = null;
 *   public ListNode(int val) {
 *     this.val = val;
 *   }
 * }
 */

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param head ListNode类
     * @return ListNode类
     */
    public ListNode oddEvenList (ListNode head) {
        //为空就不需要奇偶重排
        if (head == null) {
            return head;
        }
        ListNode even = head.next, odd = head; //odd为奇数位，even为偶数位
        //even是后行的，那么判断even和even.next为不为空就可以了
        ListNode start = even;
        while (even != null && even.next != null) {
            odd.next = even.next;//odd连接even的后一个，即奇数位
            odd = odd.next;
            even.next = odd.next;//even连接后一个奇数的后一位，即偶数位
            even = even.next;
        }
        //even整体接在odd后面
        odd.next = start;
        return head;
    }
}

BM15 删除有序链表中重复的元素-I

要求空间复杂度为O(1)

import java.util.*;

/*
 * public class ListNode {
 *   int val;
 *   ListNode next = null;
 *   public ListNode(int val) {
 *     this.val = val;
 *   }
 * }
 */

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param head ListNode类
     * @return ListNode类
     */
    public ListNode deleteDuplicates (ListNode head) {
        if (head == null) {
            return null;
        }
        ListNode last = head, result = head;
        //从第二个开始
        while (head.next != null) {
            head = head.next;
            if (last.val == head.val) {
                last.next = null;
            } else {
                last.next = head;
                last = head;
            }
        }
        return result;
    }
}

BM16 删除有序链表中重复的元素-II

进阶要求空间复杂度为O(1)

step 1：给链表前加上表头，方便可能的话删除第一个节点。
step 2：遍历链表，每次比较相邻两个节点，如果遇到了两个相邻节点相同，则新开内循环将这一段所有的相同都遍历过去。
step 3：在step 2中这一连串相同的节点前的节点直接连上后续第一个不相同值的节点。
step 4：返回时去掉添加的表头。

import java.util.*;

/*
 * public class ListNode {
 *   int val;
 *   ListNode next = null;
 *   public ListNode(int val) {
 *     this.val = val;
 *   }
 * }
 */

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param head ListNode类
     * @return ListNode类
     */
    public ListNode deleteDuplicates (ListNode head) {
        if (head == null) {
            return null;
        }
        //新加表头
        ListNode node = new ListNode(0);
        node.next = head;

        ListNode cur = node;
        //每次比较两个节点
        while (cur.next != null && cur.next.next != null) {
            if (cur.next.val == cur.next.next.val) {
                //将所有相同的都去掉
                int temp = cur.next.val;
                while (cur.next != null && cur.next.val == temp) {
                    cur.next = cur.next.next;
                }
            }else{
                cur = cur.next;
            }
        }
        return node.next;//去掉表头返回
    }
}

---

二分查找

• BM17 二分查找-I
• BM19 寻找峰值
• BM20 数组中的逆序对
• BM21 旋转数组的最小数字
• BM22 比较版本号

BM17 二分查找-I

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param nums int整型一维数组
     * @param target int整型
     * @return int整型
     */
    public int search (int[] nums, int target) {
        int result = -1;
        int left = 0, right = nums.length - 1;
        while (left <= right) {
            int mid = (left + right) / 2;
            if (nums[mid] == target) {
                result = mid;
                break;
            } else if (nums[mid] > target) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return result;
    }
}

BM19 寻找峰值

直接去寻找最大值，那么最大值一定就是峰值，这个简单，这里学习使用二分法

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param nums int整型一维数组
     * @return int整型
     */
    public int findPeakElement (int[] nums) {
        int left = 0, right = nums.length - 1;
        while (left < right) {
            int mid = left + (right - left) /
                      2; //这种写法可以防止left+right大于int的取值范围的情况出现
            //说明右边是下坡路，不一定有峰值
            if (nums[mid] > nums[mid + 1]) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return left;//最后返回left和right都可以
    }
}

BM20 数组中的逆序对

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param nums int整型一维数组
     * @return int整型
     */
    public int InversePairs (int[] nums) {
        int[] temp = new int[nums.length];
        return mergeSort(nums, 0, nums.length - 1, temp);
    }

    //先写一个归并排序，归并就是分治的思想，然后统计过程中前面比后面大的情况即可
    public int mergeSort(int[] nums, int left, int right, int[] temp) {
        if (left >= right) {
            return 0;
        }
        int mid = left + (right - left) / 2;
        int result =  mergeSort(nums, left, mid, temp) + mergeSort(nums, mid + 1, right,
                      temp);//划分
        result %= 1000000007;//防止越界
        int l = left, r = mid + 1, t = left;
        while (l <= mid && r <= right) {
            if (nums[l] > nums[r]) {
                result += mid - l + 1; //比后面的多少个都大就是mid-l
                temp[t++] = nums[r++];
            } else {
                temp[t++] = nums[l++];
            }
        }
        while (l <= mid) {
            temp[t++] = nums[l++];
        }
        while (r <= right) {
            temp[t++] = nums[r++];
        }
        for (t = left; t <= right; t++) {
            nums[t] = temp[t];
        }
        return result % 1000000007;
    }
}

BM21 旋转数组的最小数字

最简单方法就是维护最小值以O(n)的时间复杂度去找最小值呗，看下面二分法，也有双指针思想

step 1：双指针指向旋转后数组的首尾，作为区间端点。
step 2：若是区间中点值大于区间右界值，则最小的数字一定在中点右边。
step 3：若是区间中点值等于区间右界值，则是不容易分辨最小数字在哪半个区间，比如[1,1,1,0,1]，应该逐个缩减右界。
step 4：若是区间中点值小于区间右界值，则最小的数字一定在中点左边。
step 5：通过调整区间最后即可锁定最小值所在。

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param nums int整型一维数组 
     * @return int整型
     */
    public int minNumberInRotateArray (int[] nums) {
        if(nums.length==0){
            return 0;
        }
        int left =0,right = nums.length -1;
        while(left<right){
            int mid = (left+right)/2;
            //小的数字偏向右边，mid跟right指向的值相等就把right--再比较
            if(nums[mid]>nums[right]) left = mid+1;
            else if(nums[mid]<nums[right]) right = mid;
            else right--;
        }
        return nums[left];
    }
}

BM22 比较版本号

直接spilt转字符串数组，之后较短的数组不能取到内容就是为0，然后将当前需要判断的值转数字（这里易错的就是”0.226”,”0.38”比较那么0.38更大）

import java.util.*;
public class Solution {
    public int compare (String version1, String version2) {
                /*split() 方法根据匹配给定的正则表达式来拆分字符串。
注意： . 、 $、 | 和 * 等转义字符，必须得加 \\。
注意：多个分隔符，可以用 | 作为连字符。*/
        //按照.划分
        String[] nums1 = version1.split("\\."); 
        String[] nums2 = version2.split("\\.");
        for(int i = 0; i < nums1.length || i < nums2.length; i++){
            //较短的版本号后续都取0
            String str1 = i < nums1.length ? nums1[i] : "0"; 
            String str2 = i < nums2.length ? nums2[i] : "0";
            long num1 = 0;
            //字符串转数字
            for(int j = 0; j < str1.length(); j++) 
                num1 = num1 * 10 + (str1.charAt(j) - '0');
            long num2 = 0;
            for(int j = 0; j < str2.length(); j++)
                num2 = num2 * 10 + (str2.charAt(j) - '0');
            //比较数字大小
            if(num1 > num2) 
                return 1;
            if(num1 < num2)
                return -1;
        }
        //版本相同
        return 0;
    }
}

学下面的方法，主要就是转换为数字的思想

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 比较版本号
     * @param version1 string字符串
     * @param version2 string字符串
     * @return int整型
     */
    public int compare (String version1, String version2) {
        int i = 0, j = 0;
        //直到某个字符串结束
        while (i < version1.length() | j < version2.length()) {
            long num1 = 0;
            //从第一个字符串取出当前要判断的
            while (i < version1.length() && version1.charAt(i) != '.') {
                num1 = num1 * 10 + (version1.charAt(i) - '0');
                i++;
            }
            i++;//跳过点
            long num2 = 0;
            //从第二个字符串取出当前要判断的
            while (j < version2.length() && version2.charAt(j) != '.') {
                num2 = num2 * 10 + (version2.charAt(j) - '0');
                j++;
            }
            j++;//跳过点
            //比较
            if (num1 > num2) {
                return 1;
            } else if (num1 < num2) {
                return -1;
            }
        }
        //字符串相等
        return 0;
    }
}

---

二叉树

• BM23 二叉树的前序遍历
• BM24 二叉树的中序遍历
• BM25 二叉树的后序遍历
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15

BM23 二叉树的前序遍历

递归

import java.util.*;

/*
 * public class TreeNode {
 *   int val = 0;
 *   TreeNode left = null;
 *   TreeNode right = null;
 *   public TreeNode(int val) {
 *     this.val = val;
 *   }
 * }
 */

public class Solution {

    List<Integer> list = new ArrayList<>();

    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param root TreeNode类
     * @return int整型一维数组
     */
    public int[] preorderTraversal (TreeNode root) {
        List<Integer>tmp = pre(root);
        int[] ints = new int[tmp.size()];
        int i = 0;
        for (int ii : tmp) {
            ints[i++] = ii;
        }
        return ints;
    }

    List<Integer> pre(TreeNode node) {
        if (node == null) {
            return list;
        }
        list.add(node.val);
        pre(node.left);
        pre(node.right);
        return list;
    }
}

迭代

import java.util.*;

/*
 * public class TreeNode {
 *   int val = 0;
 *   TreeNode left = null;
 *   TreeNode right = null;
 *   public TreeNode(int val) {
 *     this.val = val;
 *   }
 * }
 */

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param root TreeNode类
     * @return int整型一维数组
     */
    public int[] preorderTraversal (TreeNode root) {
        if (root == null) {
            return new int[0];
        }
        ArrayList<Integer>list = new ArrayList<>();
        Stack<TreeNode>stack = new Stack<>();
        stack.push(root);//根节点入栈
        while (!stack.isEmpty()) {
            TreeNode temp = stack.pop();
            list.add(temp.val);
            //先进后出，这里就需要先放右再放左，这样就可以先拿到左节点
            if (temp.right != null) {
                stack.push(temp.right);
            }
            if (temp.left != null) {
                stack.push(temp.left);
            }
        }
        int[] ints = new int[list.size()];
        for (int i = 0; i < list.size(); i++) {
            ints[i] = list.get(i);
        }
        return ints;
    }
}

BM25 二叉树的后序遍历

递归

import java.util.*;

/*
 * public class TreeNode {
 *   int val = 0;
 *   TreeNode left = null;
 *   TreeNode right = null;
 *   public TreeNode(int val) {
 *     this.val = val;
 *   }
 * }
 */

public class Solution {

    List<Integer> list = new ArrayList<>();

    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param root TreeNode类
     * @return int整型一维数组
     */
    public int[] postorderTraversal (TreeNode root) {
        List<Integer>tmp = last(root);
        int[] ints = new int[tmp.size()];
        int i = 0;
        for (int ii : tmp) {
            ints[i++] = ii;
        }
        return ints;
    }

    List<Integer> last(TreeNode node) {
        if (node == null) {
            return list;
        }
        last(node.left);
        last(node.right);
        list.add(node.val);
        return list;
    }
}

堆/栈/队列

• BM42 用两个栈实现队列
• BM43 包含min函数的栈
• BM44 有效括号序列
• BM46 最小的K个数

BM42 用两个栈实现队列

插入直接插入stack1，需要读取的时候需要看stack2有没有内容，没有就需要将stack1的值放到stack2中，这样stack2的顶就是队列的头，也就是stack1保存新插入的值倒序，stack2保存正序的值

import java.util.*;
import java.util.Stack;

public class Solution {
    Stack<Integer> stack1 = new Stack<Integer>();
    Stack<Integer> stack2 = new Stack<Integer>();
    
    public void push(int node) {
        stack1.push(node);
    }
    
    public int pop() {
        if(stack2.size()<=0){
            while(stack1.size()!=0){
                stack2.push(stack1.pop());
            }
        }
        return stack2.pop();
    }
}

BM43 包含min函数的栈

BM43 包含min函数的栈

BM44 有效括号序列

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param s string字符串
     * @return bool布尔型
     */
    public boolean isValid (String s) {
        Stack<Character> stack = new Stack<>();
        for (int i = 0; i < s.length(); i++) {
            char c = s.charAt(i);
            if (c == '(' || c == '[' || c == '{') {
                stack.push(c);
            } else {
                if(stack.isEmpty()){
                    return false;
                }
                char tmp = stack.pop();
                if (!((tmp == '(' && c == ')') || (tmp == '[' && c == ']') || (tmp == '{' &&
                        c == '}'))) {
                    return false;
                }
            }
        }
        if (!stack.isEmpty()) {
            return false;
        }
        return true;
    }
}

BM46 最小的K个数

```







### 哈希

- <a href = "#BM51 数组中出现次数超过一半的数字">**BM51 数组中出现次数超过一半的数字**</a>
- <a href="BM52 数组中只出现一次的两个数字">**BM52 数组中只出现一次的两个数字**</a>
- <a href= "#BM53 缺失的第一个正整数">**BM53 缺失的第一个正整数**</a>



<a id="BM51 数组中出现次数超过一半的数字"></a>

**BM51 数组中出现次数超过一半的数字**

其实不用哈希，摩尔投票即可

```java
import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param numbers int整型一维数组
     * @return int整型
     */
    public int MoreThanHalfNum_Solution (int[] numbers) {
        int result = numbers[0], power = 1;
        for (int i = 1; i < numbers.length; i++) {
            if (numbers[i] != result) {
                power--;
            } else {
                power++;
            }
            if (power == 0) {
                result = numbers[i];
                power = 1;
            }
        }
        return result;
    }
}

BM52 数组中只出现一次的两个数字

借助哈希表的方式很简单，哈希表中存在这个键就移除，不存在就往里面放，这样只出现一次的键最后一定会存在于哈希表中，出现两次的就会再加入后被移除掉了

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param nums int整型一维数组
     * @return int整型一维数组
     */
    public int[] FindNumsAppearOnce (int[] nums) {
        HashMap<Integer, Object>map = new HashMap<Integer, Object>();
        for (int i : nums) {
            if (map.containsKey(i)) {
                map.remove(i, null);
            } else {
                map.put(i, null);
            }
        }
        int[] result = new int[2];
        int t = 0;
        for (Integer i : map.keySet()) {
            result[t++] = i;
        }
        return result;
    }
}

BM53 缺失的第一个正整数

空间为O(n)的方法，借助哈希表往里面插值，按照正整数从小到大查看hashmap中是否存在在哈希表中，找到最小的不在哈希表中返回即可

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param nums int整型一维数组
     * @return int整型
     */
    public int minNumberDisappeared (int[] nums) {
        int length = nums.length;
        HashMap<Integer, Integer>map = new HashMap<Integer, Integer>();
        for (int i : nums) {
            map.put(i, 1);
        }
        int result = 1;
        while (map.containsKey(result)) {
            result++;
        }
        return result;
    }
}

哈希表是一种根据关键码（key）直接访问值（value）的一种数据结构。而这种直接访问意味着只要知道key就能在O(1)时间内得到value，因此哈希表常用来统计频率、快速检验某个元素是否出现过等。

进阶（学这种），原地哈希，时间复杂度为O(n)，多次遍历数组，都是单层循环；空间复杂度为O(1)，原地哈希，以索引为指向，没有额外空间

```







### 递归/回溯

全排列问题，找出所有可能的问题，从所有可能找出一种可能，需要重复回溯的问题，答案为树状要恢复状态和线性无需恢复状态。重点就是找到满足题目要求的排除条件和递归规则条件

- **<a href="#BM55 没有重复项数字的全排列">BM55 没有重复项数字的全排列</a>**

- **<a href="#BM56 有重复项数字的全排列">BM56 有重复项数字的全排列</a>**
- **<a href="#BM57 岛屿数量">BM57 岛屿数量</a>**
- **<a href="#BM58 字符串的排列">BM58 字符串的排列</a>**
- **<a href="#BM60 括号生成">BM60 括号生成</a>**
- **<a href="#BM61 矩阵最长递增路径">BM61 矩阵最长递增路径</a>**



<a name="BM55 没有重复项数字的全排列"></a>

**BM55 没有重复项数字的全排列**

递归是一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解。因此递归过程，最重要的就是查看能不能讲原本的问题分解为更小的子问题，这是使用递归的关键。

如果是线型递归，子问题直接回到父问题不需要回溯，但是如果是树型递归，父问题有很多分支，我需要从子问题回到父问题，进入另一个子问题。因此回溯是指在递归过程中，从某一分支的子问题回到父问题进入父问题的另一子问题分支，因为有时候进入第一个子问题的时候修改过一些变量，因此回溯的时候会要求改回父问题时的样子才能进入第二子问题分支。

**思路：**

全排列就是对数组元素交换位置，使每一种排列都可能出现。因为题目要求按照字典序排列输出，那毫无疑问第一个排列就是数组的升序排列，它的字典序最小，后续每个元素与它后面的元素交换一次位置就是一种排列情况，但是如果要保持原来的位置不变，那就不应该从它后面的元素开始交换而是从自己开始交换才能保证原来的位置不变，不会漏情况。

如何保证每个元素能和从自己开始后的每个元素都交换位置，这种时候我们可以考虑递归。为什么可以使用递归？我们可以看数组[1,2,3,4]，如果遍历经过一个元素2以后，那就相当于我们确定了数组到该元素为止的前半部分，前半部分1和2的位置都不用变了，只需要对3，4进行排列，这对于后半部分而言同样是一个全排列，同样要对从每个元素开始往后交换位置，因此后面部分就是一个**子问题**。那我们考虑递归的几个条件：

- **终止条件：** 要交换位置的下标到了数组末尾，没有可交换的了，那这就构成了一个排列情况，可以加入输出数组。
- **返回值：** 每一级的子问题应该把什么东西传递给父问题呢，这个题中我们是交换数组元素位置，前面已经确定好位置的元素就是我们返还给父问题的结果，后续递归下去会逐渐把整个数组位置都确定，形成一种排列情况。
- **本级任务：** 每一级需要做的就是遍历从它开始的后续元素，每一级就与它交换一次位置。

如果只是使用递归，我们会发现，上例中的1与3交换位置以后，如果2再与4交换位置的时候，我们只能得到3412这种排列，无法得到1432这种情况。这是因为遍历的时候1与3交换位置在2与4交换位置前面，递归过程中就默认将后者看成了前者的子问题，但是其实我们1与3没有交换位置的情况都没有结束，相当于上述图示中只进行了第一个分支。因此我们用到了**回溯**。处理完1与3交换位置的子问题以后，我们再将其交换回原来的情况，相当于上述图示回到了父节点，那后续完整的情况交换我们也能得到。

```java
import java.util.*;


public class Solution {

    //交换ArrayList中两个下标的位置
    public void swap(ArrayList<Integer> list, int i1, int i2) {
        int temp = list.get(i1);
        list.set(i1, list.get(i2));
        list.set(i2, temp);
    }

    //回溯，不断交换，result保存结果，num为组合，已经按顺序排好
    public void backTrack(ArrayList<ArrayList<Integer>>result,
                          ArrayList<Integer>num, int index) {
        //结束条件是到最后一个
        if (index == num.size() - 1) {
            //注意引用，需要新建一个list
            result.add(new ArrayList<>(num));
        } else {
            //从当前位置开始是因为当前这个结果也需要保存，当前结果交换相当于不交换，之后进入递归后每次都需要交换固定的index和其他各个位置
            for (int i = index; i < num.size(); i++) {
                swap(num, i, index);
                //一开始是自己的交换，然后固定这个位置，处理index+1的部分交换，最后才跟index交换，注意是index+1
                backTrack(result, num, index + 1);
                //回溯回来再进行下个遍历
                swap(num, i, index);
            }
        }

    }

    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param num int整型一维数组
     * @return int整型ArrayList<ArrayList<>>
     */
    public ArrayList<ArrayList<Integer>> permute (int[] num) {
        //需要按照字典来，需要先排序
        Arrays.sort(num);
        ArrayList<ArrayList<Integer>>result = new ArrayList<ArrayList<Integer>>();
        //转成list
        ArrayList<Integer>list = new ArrayList<Integer>();
        for (int i = 0; i < num.length; i++) {
            list.add(num[i]);
        }
        backTrack(result, list, 0);
        return result;
    }
}

更容易理解的版本，就是每轮都选一个没填过的数字填进去，一开始排好序就可以保证字典输入了，上面那个方法空间复杂度低点，但差不多

import java.util.*;


public class Solution {
    //index控制层数，isDistance控制是否访问过，resuslt保存结果，temp保存当前内容，nums为原本内容
    public void backTrack(ArrayList<ArrayList<Integer>>result,
                          int[] nums, ArrayList<Integer>temp,
                          boolean[] isDistance, int index) {
        //找到结果
        if (index == nums.length) {
            result.add(new ArrayList<>(temp));
            return;
        }
        //对于所有数字，每次选一个加入
        for (int i = 0; i < nums.length; i++) {
            //前面已经加入过的不加入了
            if (isDistance[i]) {
                continue;
            }
            //到这里说明这个数字可以加入
            isDistance[i] = true;
            //加入
            temp.add(nums[i]);
            //递归
            backTrack(result, nums, temp, isDistance, index + 1);
            //回溯
            isDistance[i] = false;
            temp.remove(temp.size() - 1);
        }
    }

    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param num int整型一维数组
     * @return int整型ArrayList<ArrayList<>>
     */
    public ArrayList<ArrayList<Integer>> permute (int[] num) {
        //需要字典输入就先排序
        Arrays.sort(num);
        ArrayList<ArrayList<Integer>>result = new ArrayList<ArrayList<Integer>>();
        boolean[] isDistance = new boolean[num.length];
        backTrack(result, num, new ArrayList<Integer>(), isDistance, 0);
        return result;
    }
}

BM56 有重复项数字的全排列

import java.util.*;


public class Solution {
    //index
    public void backTrack(ArrayList<ArrayList<Integer>>result,
                          int[] num, boolean[] isDistance, ArrayList<Integer>temp, int index) {
        if (index == num.length) {
            result.add(new ArrayList<>(temp));
            return;
        }
        for (int i = 0; i < num.length; i++) {
            // 跳过被访问过的元素
            if (isDistance[i]) {
                continue;
            }
            //跳过相同元素以避免重复排列，这里!isDistance[i-1]是跳过上轮没有被使用的相同元素
            if (i > 0 && num[i] == num[i - 1] && !isDistance[i - 1]) {
                continue;
            }
            //加入并修改访问过
            isDistance[i] = true;
            temp.add(num[i]);
            //递归
            backTrack(result, num, isDistance, temp, index + 1);
            //回溯
            isDistance[i] = false;
            temp.remove(temp.size() - 1);
        }
    }

    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param num int整型一维数组
     * @return int整型ArrayList<ArrayList<>>
     */
    public ArrayList<ArrayList<Integer>> permuteUnique (int[] num) {
        Arrays.sort(num);
        ArrayList<ArrayList<Integer>>result = new ArrayList<ArrayList<Integer>>();
        backTrack(result, num, new boolean[num.length], new ArrayList<Integer>(), 0);
        return result;
    }
}

BM57 岛屿数量

import java.util.*;


public class Solution {
    public void backTrack(char[][] grid, int i, int j) {
        grid[i][j] = '0';
        //四个方向是否还有元素为1，有就递归置为0
        if (i > 0 && grid[i - 1][j] == '1') {
            backTrack(grid, i - 1, j);
        }
        if (i + 1 < grid.length && grid[i + 1][j] == '1') {
            backTrack(grid, i + 1, j);
        }
        if (j > 0 && grid[i][j - 1] == '1') {
            backTrack(grid, i, j - 1);
        }
        if (j + 1 < grid[0].length && grid[i][j + 1] == '1') {
            backTrack(grid, i, j + 1);
        }
    }
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 判断岛屿数量
     * @param grid char字符型二维数组
     * @return int整型
     */
    public int solve (char[][] grid) {
        int result = 0;
        int m = grid.length;
        if (m == 0) {
            return result;
        }
        int n = grid[0].length;
        if (n == 0) {
            return result;
        }
        //开始遍历，每次找到一个为1的位置就把相连的位置修改为0，不用修改回来
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == '1') {
                    result++;
                    //修改相邻的
                    backTrack(grid, i, j);
                }
            }
        }
        return result;
    }
}

BM58 字符串的排列

import java.util.*;


public class Solution {

    public void backTrack(ArrayList<String>result,
                          String str, StringBuilder temp, boolean[] isDistance, int index) {
        if (index == str.length()) {
            result.add(new String(temp));
            return;
        }
        for (int i = 0; i < str.length(); i++) {
            //访问过就不访问了
            if (isDistance[i]) {
                continue;
            }
            //出现相同的不处理
            if (i > 0 && str.charAt(i - 1) == str.charAt(i) && !isDistance[i - 1]) {
                continue;
            }
            temp.append(str.charAt(i));
            isDistance[i] = true;
            backTrack(result, str, temp, isDistance, index + 1);
            temp.deleteCharAt(temp.length() - 1);
            isDistance[i] = false;
        }
    }

    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param str string字符串
     * @return string字符串ArrayList
     */
    public ArrayList<String> Permutation (String str) {
        ArrayList<String> result = new ArrayList<String>();
        char[] chars = str.toCharArray();
        Arrays.sort(chars); // 先排序
        backTrack(result, new String(chars), new StringBuilder(),
                  new boolean[str.length()], 0);
        return result;
    }
}

BM60 括号生成

import java.util.*;


public class Solution {
    public void backTrack(int left, int right, ArrayList<String>result,
                          String temp, int n) {
        //找到结果就是左括号数量等于右括号的数量
        if (left == n && right == n) {
            result.add(temp);
            return;
        }
        //还可以加左括号就加
        if (left < n) {
            backTrack(left + 1, right, result, temp + "(", n);
        }
        //还可以加右括号并且当前右括号数量小于左括就可以加
        if (right < n && left > right) {
            backTrack(left, right + 1, result, temp + ")", n);
        }
    }
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param n int整型
     * @return string字符串ArrayList
     */
    public ArrayList<String> generateParenthesis (int n) {
        ArrayList<String>result = new ArrayList<String>();
        backTrack(0, 0, result, "", n);
        return result;
    }
}

简单好理解，没有缓存

import java.util.*;

public class Solution {

    int result = 0;

    public void backTrack(int i, int j, int[][] matrix,
                          int last, int index) {
        // 越界，或者已经访问过
        if (i < 0 || i >= matrix.length || j < 0 || j >= matrix[0].length  ||
                matrix[i][j] <= last) {
            result = Math.max(result, index);
            return;
        }
        // 向上下左右四个方向递归
        backTrack(i - 1, j, matrix, matrix[i][j], index + 1);
        backTrack(i + 1, j, matrix, matrix[i][j], index + 1);
        backTrack(i, j - 1, matrix, matrix[i][j], index + 1);
        backTrack(i, j + 1, matrix, matrix[i][j], index + 1);
    }

    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 递增路径的最大长度
     * @param matrix int整型二维数组 描述矩阵的每个数
     * @return int整型
     */
    public int solve(int[][] matrix) {
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix[0].length; j++) {
                backTrack(i, j, matrix, -1, 0);
            }
        }
        return result;
    }
}

动态规划

• BM62 斐波那契数列

• BM63 跳台阶

• BM64 最小花费爬楼梯 （关注一下，初始化状态的不同和处理）

BM62 斐波那契数列

递归

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param n int整型
     * @return int整型
     */
    public int Fibonacci (int n) {
        if (n <= 2) {
            return 1;
        }
        return Fibonacci(n - 1) + Fibonacci(n - 2);
    }
}

迭代

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param n int整型
     * @return int整型
     */
    public int Fibonacci (int n) {
        if (n <= 2) {
            return 1;
        }
        int first = 1, second = 1;
        for (int i = 2; i < n; i++) {
            int temp = first + second;
            first = second;
            second = temp;
        }
        return second;
    }
}

BM63 跳台阶

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param number int整型
     * @return int整型
     */
    public int jumpFloor (int number) {
        int first = 1, second = 1;
        for (int i = 2; i <= number; i++) {
            int temp = first + second;
            first = second;
            second = temp;
        }
        return second;
    }
}

BM64 最小花费爬楼梯

• step 1：可以用一个数组记录每次爬到第i阶楼梯的最小花费，然后每增加一级台阶就转移一次状态，最终得到结果。
• step 2：（初始状态） 因为可以直接从第0级或是第1级台阶开始，因此这两级的花费都直接为0.
• step 3：（状态转移） 每次到一个台阶，只有两种情况，要么是它前一级台阶向上一步，要么是它前两级的台阶向上两步，因为在前面的台阶花费我们都得到了，因此每次更新最小值即可，转移方程为：dp[i]=min(dp[i−1]+cost[i−1],dp[i−2]+cost[i−2])。

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param cost int整型一维数组
     * @return int整型
     */
    public int minCostClimbingStairs (int[] cost) {
        //dp表示爬到第i级台阶需要的最小花费，这里+1是为了更容易满足下面的转移方程，不再需要额外处理越界
        int[] dp = new int[cost.length + 1];
        for (int i = 2; i <= cost.length; i++) {
            dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
        }
        return dp[cost.length];
    }
}

<a name=””

字符串

• BM83 字符串变形
• BM84 最长公共前缀
• BM85 验证IP地址
• BM86 大数加法

BM83 字符串变形

用内置函数的reverse()翻转也可以

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param s string字符串
     * @param n int整型
     * @return string字符串
     */
    public String trans (String s, int n) {
        char[] result = new char[n];
        int count = 0;
        for (int i = n - 1; i >= 0; i--) {
            int j = i;//j为当前检索的单词的前面
            while (j >= 0 && s.charAt(j) != ' ') {
                j--;
            }
            String temp = s.substring(j + 1, i + 1);
            for (int k = 0; k < temp.length(); k++) {
                char c = temp.charAt(k);
                if (c >= 'A' && c <= 'Z') {
                    c = ((char)(c - 'A' + 'a'));
                } else {
                    c = ((char)(c + 'A' - 'a'));
                }
                result[count++] = c;
            }
            if (count < result.length) {
                result[count++] = ' ';
            }
            i = j;
        }
        return new String(result);
    }
}

BM84 最长公共前缀

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param strs string字符串一维数组
     * @return string字符串
     */
    public String longestCommonPrefix (String[] strs) {
        if (strs.length == 0) {
            return "";
        }
        int largest = 0, target = 0;
        //找到最长的字符串
        for (int i = 0; i < strs.length; i++) {
            if (strs[i].length() > largest) {
                largest = strs[i].length();
                target = i;
            }
        }
        int index = 0;
        for (int i = 0; i < largest; i++) {
            char c = strs[target].charAt(i);
            for (int j = 0; j < strs.length; j++) {
                if ((strs[j].length() > i && strs[j].charAt(i) == c) || j == target) {
                    continue;
                }
                return strs[target].substring(0, i);
            }
        }
        return strs[target].substring(0, strs[target].length());
    }
}

BM85 验证IP地址

```





<a id="BM86 大数加法"></a>

**BM86 大数加法**

```java

双指针

• BM88 判断是否为回文字符串
• BM89 合并区间
• BM91 反转字符串
• BM92 最长无重复子数组
• BM93 盛水最多的容器

BM88 判断是否为回文字符串

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param str string字符串 待判断的字符串
     * @return bool布尔型
     */
    public boolean judge (String str) {
        int left = 0, right = str.length() - 1;
        while (left < right) {
            if (str.charAt(left++) != str.charAt(right--)) {
                return false;
            }
        }
        return true;
    }
}

BM89 合并区间

跟主持人调度很像，排序+贪心，下面是个人想法

其实就是找交叉区间

import java.util.*;

/*
 * public class Interval {
 *   int start;
 *   int end;
 *   public Interval(int start, int end) {
 *     this.start = start;
 *     this.end = end;
 *   }
 * }
 */

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param intervals Interval类ArrayList
     * @return Interval类ArrayList
     */
    public ArrayList<Interval> merge (ArrayList<Interval> intervals) {
        ArrayList<Interval> result = new ArrayList<>();
        if (!intervals.isEmpty()) {
            int[] start = new int[intervals.size()];
            int[] end = new int[intervals.size()];
            for (int i = 0; i < intervals.size(); i++) {
                start[i] = intervals.get(i).start;
                end[i] = intervals.get(i).end;
            }
            Arrays.sort(start, 0, start.length);
            Arrays.sort(end, 0, end.length);
            int left_value = start[0], right_value = end[0];
            for (int left = 1, right = 1; left < start.length; left++, right++) {
                if (start[left] > right_value) {
                    result.add(new Interval(left_value, right_value));
                    left_value = start[left];
                    right_value = end[right];
                } else {
                    if (end[right] > right_value) {
                        right_value = end[right];
                    }
                }
            }
            result.add(new Interval(left_value, right_value));
        }
        return result;
    }
}

BM91 反转字符串

直接复制一个数组然后逆序放到新数组

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 反转字符串
     * @param str string字符串
     * @return string字符串
     */
    public String solve (String str) {
        char[] result = str.toCharArray();
        int len = str.length();
        for (int i = 0; i < len; i++) {
            result[len - 1 - i] = str.charAt(i);
        }
        return new String(result);
    }
}

减少操作时间

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 反转字符串
     * @param str string字符串 
     * @return string字符串
     */
    public String solve (String str) {
        char[] result = str.toCharArray();
        int len = str.length();
        for(int i = 0;i<len/2;i++){
            char temp = str.charAt(i);
            result[i] = result[len-1-i];
            result[len-1-i] = temp;
        }
        return new String(result);
    }
}

BM92 最长无重复子数组

我们使用两个指针，一个i一个j，最开始的时候i和j指向第一个元素，然后i往后移，把扫描过的元素都放到map中，如果i扫描过的元素没有重复的就一直往后移，顺便记录一下最大值max，如果i扫描过的元素有重复的，就改变j的位置

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param arr int整型一维数组 the array
     * @return int整型
     */
    public int maxLength (int[] arr) {
        //可以用hashMap，queue，set，反正思路都是一样的
        int max = 0;
        Set<Integer>set = new HashSet<>();
        int left = 0, right = 0;
        while (right < arr.length) {
            if (set.contains(arr[right])) {
                set.remove(arr[left++]);
            } else {
                set.add(arr[right++]);
                max = Math.max(max, set.size());
            }
        }
        return max;
    }
}

BM93 盛水最多的容器

双指针指的是在遍历对象的过程中，不是普通的使用单个指针进行访问，而是使用两个指针（特殊情况甚至可以多个），两个指针或是同方向访问两个链表、或是同方向访问一个链表（快慢指针）、或是相反方向扫描（对撞指针），从而达到我们需要的目的。

这里还有贪心思想，贪心策略是每次移动的指针是移动指针指向的高度较短的那个

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param height int整型一维数组
     * @return int整型
     */
    public int maxArea (int[] height) {
        int max = 0 ;
        //优先排除特殊情况
        if (height.length < 2) {
            return 0;
        }
        int left = 0, right = height.length - 1;
        while (left < right) {
            if ((right - left) * Math.min(height[right], height[left]) > max) {
                max = (right - left) * Math.min(height[right], height[left]) ;
            }
            //贪心，移动较短的那个
            if (height[right] > height[left]) {
                left++;
            } else {
                right--;
            }
        }
        return max;
    }
}

贪心算法

• BM96 主持人调度（二）

BM96 主持人调度（二）

贪心思想属于动态规划思想中的一种，其基本原理是找出整体当中给的每个局部子结构的最优解，并且最终将所有的这些局部最优解结合起来形成整体上的一个最优解。

我们利用贪心思想，什么时候需要的主持人最少？那肯定是所有的区间没有重叠，每个区间首和上一个的区间尾都没有相交的情况，我们就可以让同一位主持人不辞辛劳，一直主持了。但是题目肯定不是这种理想的情况，那我们需要对交叉部分，判断需要增加多少位主持人。

step 1: 利用辅助数组获取单独各个活动开始的时间和结束时间，然后分别开始时间和结束时间进行排序，方便后面判断是否相交。
step 2: 遍历n个活动，如果某个活动开始的时间大于之前活动结束的时候，当前主持人就够了，活动结束时间往后一个。
step 3: 若是出现之前活动结束时间晚于当前活动开始时间的，则需要增加主持人。

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 计算成功举办活动需要多少名主持人
     * @param n int整型 有n个活动
     * @param startEnd int整型二维数组 startEnd[i][0]用于表示第i个活动的开始时间，startEnd[i][1]表示第i个活动的结束时间
     * @return int整型
     */
    public int minmumNumberOfHost (int n, int[][] startEnd) {
        int need_people = 0;
        int[] start = new int[n];
        int[] end = new int[n];
        //分别得到活动起始时间
        for (int i = 0; i < n; i++) {
            start[i] = startEnd[i][0];
            end[i] = startEnd[i][1];
        }
        //单独排序
        Arrays.sort(start, 0, start.length);
        Arrays.sort(end, 0, end.length);
        //
        int j = 0;
        for (int i = 0; i < n; i++) {
            //新开始的节目大于上一轮结束的时间，主持人不变
            if (start[i] >= end[j]) {
                j++;
            } else {
                //增加主持人
                need_people++;
            }
        }
        return need_people;
    }
}

模拟

• BM97旋转数组
• BM99 顺时针旋转矩阵
• BM100 设计LRU缓存结构
• BM101 设计LFU缓存结构

BM97旋转数组

方法一：使用额外数组，然后遍历每个数字放到正确位置后返回数组

方法二：三次翻转（推荐使用）

循环右移相当于从第m个位置开始，左右两部分视作整体翻转。即abcdefg右移3位efgabcd可以看成AB翻转成BA（这里小写字母看成数组元素，大写字母看成整体）。既然是翻转我们就可以用到reverse函数。

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 旋转数组
     * @param n int整型 数组长度
     * @param m int整型 右移距离
     * @param a int整型一维数组 给定数组
     * @return int整型一维数组
     */
    public int[] solve (int n, int m, int[] a) {
        //取模，比n长有n是没有作用的移动
        m = m % n;
        //第一次全部逆转
        reverse(a, 0, n - 1);
        //第二次逆转开头m个
        reverse(a, 0, m - 1);
        //第三次逆转m后所有元素
        reverse(a, m, n - 1);
        return a;
    }

    public void reverse(int[] a, int start, int end) {
        while (start < end) {
            int temp = a[start];
            a[start] = a[end];
            a[end] = temp;
            start++;
            end--;
        }
    }
}

BM99 顺时针旋转矩阵

方法一：直接复制一个二维数组填入返回即可，第i行换到第n-i列(关系是初始位置的横坐标+换后的纵坐标=n)，换之前的纵坐标和换之后的横坐标相等

方法二：沿右下对角线翻转，再左右翻转；也可以沿左上对角线翻转，再上下翻转

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param mat int整型二维数组 
     * @param n int整型 
     * @return int整型二维数组
     */
    public int[][] rotateMatrix (int[][] mat, int n) {
        if(n!=0){
            diagonalReverse(mat,n);
            leftRightReverse(mat,n);
        }
        return mat;
    }

    //上下翻转，用不上，顺便写出来了
    public void upDownReverse(int[][]mat,int n){
        for(int i = 0;i<n/2;i++){
            for(int j = 0;j<n;j++){
                int temp = mat[i][j];
                mat[i][j] = mat[n-1-i][j];
                mat[n-1-i][j] = temp;
            }
        }
    }

    //左右翻转
    public void leftRightReverse(int[][]mat,int n){
        for(int i = 0;i<n;i++){
            for(int j = 0;j<n/2;j++){
                int temp = mat[i][j];
                mat[i][j] = mat[i][n-1-j];
                mat[i][n-1-j] = temp;
            }
        }
    }

    //沿右下对角线翻转
    public void diagonalReverse(int[][]mat,int n){
        for(int i = 0;i<n;i++){
            for(int j = i+1;j<n;j++){
                int temp = mat[i][j];
                mat[i][j] = mat[j][i];
                mat[j][i] = temp;
            }
        }
    }
}

BM100 设计LRU缓存结构

BM101 设计LFU缓存结构