代码随想录学习记录

数组

双指针思想

二分查找

这道题目的前提是数组为有序数组，同时题目还强调数组中无重复元素，因为一旦有重复元素，使用二分查找法返回的元素下标可能不是唯一的，这些都是使用二分法的前提条件，当大家看到题目描述满足如上条件的时候，可要想一想是不是可以用二分法了。

704. 二分查找

704. 二分查找 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int search(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        // 左闭右闭
        while (left <= right) {
            int mid = left + ((right - left) >> 1);
            // 小于，目标值在右边，left往右边跑
            if (nums[mid] < target) {
                left = mid + 1;
            }
            // 大于，目标值在左边，right往左边跑
            else if (nums[mid] > target) {
                right = mid - 1;
            }
            // 相等
            else {
                return mid;
            }
        }
        return -1;
    }
}

35. 搜索插入位置

35. 搜索插入位置 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public int searchInsert(int[] nums, int target) {
         int left = 0, right = nums.length - 1;
        // 左闭右闭
        while (left <= right) {
            int mid = left + ((right - left) >> 1);
            // 小于，需要插入的位置在右边，left往右边跑
            if (nums[mid] < target) {
                left = mid + 1;
            }
            // 大于，需要插入的位置在左边，right往左边跑
            else if (nums[mid] > target) {
                right = mid - 1;
            }
            // 相等直接在相等的位置插入
            else {
                return mid;
            }
        }
        //最后没找到相等的，left和right错开的位置结束了循环，是最接近target的位置，根据推算，返回left位置即可
        return left;
    }
}

34. 在排序数组中查找元素的第一个和最后一个位置

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public int[] searchRange(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        // 左闭右闭
        while (left <= right) {
            int mid = left + ((right - left) >> 1);
            // 小于，需要插入的位置在右边，left往右边跑
            if (nums[mid] < target) {
                left = mid + 1;
            }
            // 大于，需要插入的位置在左边，right往左边跑
            else if (nums[mid] > target) {
                right = mid - 1;
            }

            // 相等就看左右哪个不相等就移动一个位置就好，不然就结束循环
            else {
                if (nums[left] != nums[mid]) {
                    left++;
                } else if (nums[right] != nums[mid]) {
                    right--;
                } else {
                    return new int[] { left, right };
                }
            }
        }
        // 最后没找到相等的，或者nums为空
        return new int[] { -1, -1 };
    }
}

**69. x 的平方根 **

69. x 的平方根 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int mySqrt(int x) {
        int left = 0, right = x, result = -1;
        while (left <= right) {
            int mid = left + ((right - left) >> 1);
            long square = (long) mid * mid;  // 使用 long 防止溢出
            // 如果 mid * mid 小于 x，向右侧逼近
            if (square < x) {
                left = mid + 1;
            } else if (square > x) {
                // 如果 mid * mid 大于 x，向左侧逼近
                right = mid - 1;
            } else {
                // 如果正好等于 x，直接返回 mid
                return mid;
            }
        }
        // 最终返回的是最大的满足 mid*mid <= x 的 mid
        return right; // right 会是最接近但不大于 x 平方根的值
    }
}

367. 有效的完全平方数

367. 有效的完全平方数 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public boolean isPerfectSquare(int num) {
        int left = 0, right = num;
        while (left <= right) {
            int mid = left + ((right - left) >> 1);
            if ((long) mid * mid < num) {
                // 左指针向右移动尝试
                left = mid + 1;
            } else if ((long) mid * mid > num) {
                // 右指针向左移动尝试
                right = mid - 1;
            } else {
                // 相等直接返回true
                return true;
            }
        }
        // 走到这里说明只有逼近值，right，但是没有能够完全想等的
        return false;
    }
}

双指针

27. 移除元素

27. 移除元素 - 力扣（LeetCode）

双指针解决，快慢指针

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int removeElement(int[] nums, int val) {
        // 相等的个数
        int count = 0;
        // 记录当前插入的下标
        int index = 0;
        // 记录当前遍历到的位置
        int i = 0;
        while (i <= nums.length - 1) {
            // 相等就i跳过，但是index不跳过，下次遇到不相等的插入到index就好
            if (nums[i] == val) {
                i++;
            }
            // 不相等就插入当前位置到index的位置，两个都加1
            else {
                nums[index++] = nums[i++];
                count++;
            }
        }
        return count;
    }
}

26. 删除有序数组中的重复项

26. 删除有序数组中的重复项 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public int removeDuplicates(int[] nums) {
        //遇到相同的就直接跳过就好
        if(nums.length==0){
            return 0;
        }
        //不同元素的个数
        int count = 1;
        //上次的元素
        int lastDifferent = nums[0];
        //能够插入的位置
        int slow = 1;
        //快慢指针
        for(int fast = 1;fast<nums.length;fast++){
            if(nums[fast]!=lastDifferent){
                lastDifferent = nums[fast];
                  nums[slow++] = nums[fast];
                  count++;
            }
        }
        return count;
    }
}

283. 移动零

283. 移动零 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public void moveZeroes(int[] nums) {
        // 能够插入的位置
        int slow = 0;
        // 快慢指针
        for (int fast = 0; fast < nums.length; fast++) {
            if (nums[fast] != 0) {
                nums[slow++] = nums[fast];
            }
        }
        // 余下填充0
        while (slow <= nums.length - 1) {
            nums[slow++] = 0;
        }
    }
}

844. 比较含退格的字符串

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
class Solution {
    public boolean backspaceCompare(String s, String t) {
        // #会导致回退，可以倒序双指针比较
        int i = s.length() - 1, j = t.length() - 1;
        int skipS = 0, skipT = 0;
        while (i >= 0 || j >= 0) {
            // 先处理s
            while (i >= 0) {
                if (s.charAt(i) == '#') {
                    // 删除一个元素，但是可能存在多个，这里先保存需要删除多少个
                    skipS++;
                    i--;
                } else if (skipS > 0) {
                    // 需要删除
                    skipS--;
                    i--;
                } else {
                    // 到这里说明这个元素是最后存在的
                    break;
                }
            }
            // 同理处理t
            while (j >= 0) {
                if (t.charAt(j) == '#') {
                    // 删除一个元素，但是可能存在多个，这里先保存需要删除多少个
                    skipT++;
                    j--;
                } else if (skipT > 0) {
                    // 需要删除
                    skipT--;
                    j--;
                } else {
                    // 到这里说明这个元素是最后存在的
                    break;
                }
            }
            // 看是不是两个都在正常位置
            if (i >= 0 && j >= 0) {
                if (s.charAt(i) != t.charAt(j)) {
                    return false;
                }
            }
            // 访问到超出范围的情况，但是有一个还是能取到元素就说明不相等
            else {
                if (i >= 0 || j >= 0) {
                    return false;
                }
            }
            // 比较到两个相等的一个位置了，整体前移动继续比较
            i--;
            j--;
        }
        return true;
    }
}

977. 有序数组的平方

977. 有序数组的平方 - 力扣（LeetCode）

还可以就是先全部平方，然后一个sort搞定，就是原地操作了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int[] sortedSquares(int[] nums) {
        int left = 0, right = nums.length - 1;
        int[] result = new int[nums.length];
        int i = result.length - 1;
        while (left <= right) {
            if (nums[left] * nums[left] < nums[right] * nums[right]) {
                result[i--] = nums[right] * nums[right];
                right--;
            } else {
                result[i--] = nums[left] * nums[left];
                left++;
            }
        }
        return result;
    }
}

滑动窗口

209. 长度最小的子数组

209. 长度最小的子数组 - 力扣（LeetCode）

在暴力解法中，是一个for循环滑动窗口的起始位置，一个for循环为滑动窗口的终止位置，用两个for循环 完成了一个不断搜索区间的过程。

那么滑动窗口如何用一个for循环来完成这个操作呢。

首先要思考 如果用一个for循环，那么应该表示 滑动窗口的起始位置，还是终止位置。

如果只用一个for循环来表示 滑动窗口的起始位置，那么如何遍历剩下的终止位置？

此时难免再次陷入 暴力解法的怪圈。

所以 只用一个for循环，那么这个循环的索引，一定是表示 滑动窗口的终止位置。

窗口就是 满足其和 ≥ s 的长度最小的 连续 子数组。

窗口的起始位置如何移动：如果当前窗口的值大于等于s了，窗口就要向前移动了（也就是该缩小了）。

窗口的结束位置如何移动：窗口的结束位置就是遍历数组的指针，也就是for循环里的索引。

可以发现滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        // 暴力解法就是On^2会超时，这里用双指针的滑动窗口，时间复杂度On 严格是O2n
        //保存结果
        int result = Integer.MAX_VALUE;
        //保存当前计算区间内的和
        int sum = 0;
        //左指针
        int left  = 0;
        for(int right = 0;right<nums.length;right++){
            sum+=nums[right];
            //如果出现区间内的和大于等于就可以移动左指针缩小区间了
            while(sum>=target){
                //先保存结果再缩小区间
                result = Math.min(result,right-left+1);
                sum-=nums[left++];
            }
        }

        return result == Integer.MAX_VALUE ? 0 : result;
    }
}

904. 水果成篮

904. 水果成篮 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int totalFruit(int[] fruits) {
        int result = 0;
        int left = 0;
        // 定义一个哈希表来保证只存在两个不同的值，也就是不同的篮子
        HashMap<Integer, Integer> map = new HashMap<>();
        for (int right = 0; right < fruits.length; right++) {
            // 先往哈希表里面放
            map.put(fruits[right], map.getOrDefault(fruits[right], 0) + 1);
            // 看哈希表是不是超过2个篮子,超过两个篮子，就不断移动left删除元素，直到篮子符合要求
            while (map.size() > 2) {
                map.put(fruits[left], map.get(fruits[left]) - 1);
                if (map.get(fruits[left]) == 0) {
                    map.remove(fruits[left]);
                }
                ++left;
            }
            result = Math.max(result, right - left + 1);
        }
        return result;
    }
}

76. 最小覆盖子串

76. 最小覆盖子串 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution {

    HashMap<Character, Integer> map1 = new HashMap<>();
    HashMap<Character, Integer> map2 = new HashMap<>();

    public String minWindow(String s, String t) {
        // 把目标值的不同字符的数量保存到map
        for (int i = 0; i < t.length(); i++) {
            map1.put(t.charAt(i), map1.getOrDefault(t.charAt(i), 0) + 1);
        }

        int left = 0;
        // len保存最小满足条件的长度,l为答案的左边，r为答案右边
        int len = Integer.MAX_VALUE, l = -1, r = -1;
        for (int right = 0; right < s.length(); right++) {
            // t存在这个字符
            if (map1.containsKey(s.charAt(right))) {
                map2.put(s.charAt(right), map2.getOrDefault(s.charAt(right), 0) + 1);
            }
            // 满足情况下移动左指针
            while (check() && left <= right) {
                if (right - left + 1 < len) {
                    len = right - left + 1;
                    l = left;
                    r = right;
                }
                if (map1.containsKey(s.charAt(left))) {
                    map2.put(s.charAt(left), map2.getOrDefault(s.charAt(left), 0) - 1);
                }
                left++;
            }
        }
        return l == -1 ? "" : s.substring(l, r + 1);
    }

    // 检查map2是否都包含map1的值和数量
    public boolean check() {
        for (Map.Entry<Character, Integer> entry : map1.entrySet()) {
            if (map2.getOrDefault(entry.getKey(), 0) < entry.getValue()) {
                return false;
            }
        }
        return true;
    }
}

模拟 螺旋

59. 螺旋矩阵 II

59. 螺旋矩阵 II - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    public int[][] generateMatrix(int n) {
        int[][] result = new int[n][n];

        int top = 0, bottom = n - 1, left = 0, right = n - 1;
        int i = 0, j = 0, temp = 1;
        while (top <= bottom && left <= right) {
            // 向右
            for (int k = left; k <= right; k++) {
                result[top][k] = temp++;
            }
            top++;
            // 向下
            for (int k = top; k <= bottom; k++) {
                result[k][right] = temp++;
            }
            right--;
            // 向左
            for (int k = right; k >= left; k--) {
                result[bottom][k] = temp++;
            }
            bottom--;
            // 向上
            for (int k = bottom; k >= top; k--) {
                result[k][left] = temp++;
            }
            left++;
        }

        return result;
    }
}

54. 螺旋矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        // 行数量
        int row = matrix.length;
        if (row == 0) {
            return new ArrayList<Integer>();
        }
        // 列数
        int column = matrix[0].length;
        // 保存结果
        List<Integer> result = new ArrayList<>();
        // 保存当前外围范围
        int top = 0, bottom = row - 1, left = 0, right = column - 1;
        // 这里的条件要改为 &&，保证同时检查行和列的边界
        while (top <= bottom && left <= right) {
            // 向右和向下一开始保证了，但向左和向上没有，并且是反向的需要在循环中进行判断
            // 向右
            for (int k = left; k <= right; k++) {
                result.add(matrix[top][k]);
            }
            top++;
            // 向下
            for (int k = top; k <= bottom; k++) {
                result.add(matrix[k][right]);
            }
            right--;
            // 向左
            if (top <= bottom) {
                for (int k = right; k >= left; k--) {
                    result.add(matrix[bottom][k]);
                }
                bottom--;
            }
            // 向上
            if (left <= right) {
                for (int k = bottom; k >= top; k--) {
                    result.add(matrix[k][left]);
                }
                left++;
            }
        }
        return result;
    }
}

LCR 146. 螺旋遍历二维数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
    public int[] spiralArray(int[][] array) {
        // 行数量
        int row = array.length;
        if (row == 0) {
            return new int[0];
        }
        // 列数
        int column = array[0].length;
        // 保存结果
        int[] result = new int[row * column];
        // 保存当前外围范围
        int top = 0, bottom = row - 1, left = 0, right = column - 1;
        // 保存结果当前填充到哪个下标
        int temp = 0;

        // 这里的条件要改为 &&，保证同时检查行和列的边界
        while (top <= bottom && left <= right) {
            // 向右和向下一开始保证了，但向左和向上没有，并且是反向的需要在循环中进行判断
            // 向右
            for (int k = left; k <= right; k++) {
                result[temp++] = array[top][k];
            }
            top++;
            // 向下
            for (int k = top; k <= bottom; k++) {
                result[temp++] = array[k][right];
            }
            right--;
            // 向左
            if (top <= bottom) {
                for (int k = right; k >= left; k--) {
                    result[temp++] = array[bottom][k];
                }
                bottom--;
            }
            // 向上
            if (left <= right) {
                for (int k = bottom; k >= top; k--) {
                    result[temp++] = array[k][left];
                }
                left++;
            }
        }
        return result;
    }
}

前缀和

区间和

第一行输入为整数数组 Array 的长度 n，接下来 n 行，每行一个整数，表示数组的元素。随后的输入为需要计算总和的区间下标：a，b （b > = a），直至文件结束。

1
2
3
4
5
6
7
8
5
1
2
3
4
5
0 1
1 3
1
2
3
9

如果，我们想统计，在vec数组上 下标 2 到下标 5 之间的累加和，那是不是就用 p[5] - p[1] 就可以了。

为什么呢？

p[1] = vec[0] + vec[1];
p[5] = vec[0] + vec[1] + vec[2] + vec[3] + vec[4] + vec[5];
p[5] - p[1] = vec[2] + vec[3] + vec[4] + vec[5];

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);

        int n = scanner.nextInt();
        int[] vec = new int[n];
        int[] p = new int[n];

        int presum = 0;
        for (int i = 0; i < n; i++) {
            vec[i] = scanner.nextInt();
            presum += vec[i];
            p[i] = presum;
        }

        while (scanner.hasNextInt()) {
            int a = scanner.nextInt();
            int b = scanner.nextInt();

            int sum;
            if (a == 0) {
                sum = p[b];
            } else {
                sum = p[b] - p[a - 1];
            }
            System.out.println(sum);
        }

        scanner.close();
    }
}

开发商购买土地

在一个城市区域内，被划分成了n * m个连续的区块，每个区块都拥有不同的权值，代表着其土地价值。目前，有两家开发公司，A 公司和 B 公司，希望购买这个城市区域的土地。

现在，需要将这个城市区域的所有区块分配给 A 公司和 B 公司。

然而，由于城市规划的限制，只允许将区域按横向或纵向划分成两个子区域，而且每个子区域都必须包含一个或多个区块。

为了确保公平竞争，你需要找到一种分配方式，使得 A 公司和 B 公司各自的子区域内的土地总价值之差最小。

注意：区块不可再分。

【输入描述】

第一行输入两个正整数，代表 n 和 m。

接下来的 n 行，每行输出 m 个正整数。

输出描述

请输出一个整数，代表两个子区域内土地总价值之间的最小差距。

【输入示例】

3 3 1 2 3 2 1 3 1 2 3

【输出示例】

0

【提示信息】

如果将区域按照如下方式划分：

1 2 | 3 2 1 | 3 1 2 | 3

两个子区域内土地总价值之间的最小差距可以达到 0。

【数据范围】：

  • 1 <= n, m <= 100；
  • n 和 m 不同时为 1。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int m = scanner.nextInt();
        int sum = 0;
        int[][] vec = new int[n][m];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                vec[i][j] = scanner.nextInt();
                sum += vec[i][j];
            }
        }

        // 统计横向
        int[] horizontal = new int[n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                horizontal[i] += vec[i][j];
            }
        }

        // 统计纵向
        int[] vertical = new int[m];
        for (int j = 0; j < m; j++) {
            for (int i = 0; i < n; i++) {
                vertical[j] += vec[i][j];
            }
        }

        int result = Integer.MAX_VALUE;
        int horizontalCut = 0;
        for (int i = 0; i < n; i++) {
            horizontalCut += horizontal[i];
            result = Math.min(result, Math.abs(sum - 2 * horizontalCut));
        }

        int verticalCut = 0;
        for (int j = 0; j < m; j++) {
            verticalCut += vertical[j];
            result = Math.min(result, Math.abs(sum - 2 * verticalCut));
        }

        System.out.println(result);
        scanner.close();
    }
}

链表

  • 链表的种类主要为：单链表，双链表，循环链表
  • 链表的存储方式：链表的节点在内存中是分散存储的，通过指针连在一起。
  • 链表是如何进行增删改查的。
  • 数组和链表在不同场景下的性能分析。

虚拟头节点

203. 移除链表元素

https://leetcode.cn/problems/remove-linked-list-elements/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/**
 * Definition for singly-linked list.
 * public class ListNode {
 * int val;
 * ListNode next;
 * ListNode() {}
 * ListNode(int val) { this.val = val; }
 * ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode removeElements(ListNode head, int val) {
        ListNode result = null;
        ListNode last = null;
        while (head != null) {
            //不相等才处理
            if (head.val != val) {
                //第一个保存为结果
                if (result == null) {
                    result = head;
                }
                //第一个和已经有的
                if (last == null) {
                    last = head;
                } else {
                    last.next = head;
                    last = last.next;
                }
            }
            head = head.next;
        }
        // 最后一个元素若存在置空
        if (last != null) {
            last.next = null;
        }
        return result;
    }
}

看下面虚拟节点的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * Definition for singly-linked list.
 * public class ListNode {
 * int val;
 * ListNode next;
 * ListNode() {}
 * ListNode(int val) { this.val = val; }
 * ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode removeElements(ListNode head, int val) {
        // 虚拟头节点，逻辑更清楚
        ListNode newHead = new ListNode();
        newHead.next = head;
        ListNode cur = newHead;
        while (cur.next != null) {
            if (cur.next.val == val) {
                cur.next = cur.next.next;
            } else {
                cur = cur.next;
            }
        }
        return newHead.next;
    }
}

链表的基本操作

707. 设计链表

707. 设计链表 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
class ListNode {
    int val;
    ListNode next;

    ListNode() {

    }

    ListNode(int val) {
        this.val = val;
    }
}

class MyLinkedList {

    // 真实节点数量，不包括虚拟头节点
    private int size;
    // 虚拟头节点
    private ListNode head;

    public MyLinkedList() {
        size = 0;
        head = new ListNode();
    }

    public int get(int index) {
        // size为下标，从0开始
        if (index < 0 || index >= size) {
            return -1;
        }
        ListNode result = head;
        for (int i = 0; i <= index; i++) {
            result = result.next;
        }
        return result.val;
    }

    public void addAtHead(int val) {
        // 添加到头就是插入在虚拟节点后面，原本虚拟节点后面的值放在新节点后面
        ListNode newNode = new ListNode(val);
        ListNode next = head.next;
        head.next = newNode;
        newNode.next = next;
        size++;
    }

    public void addAtTail(int val) {
        // 添加到尾就是直接遍历节点，添加到尾部
        ListNode temp = head;
        for (int i = 0; i < size; i++) {
            temp = temp.next;
        }
        temp.next = new ListNode(val);
        size++;
    }

    public void addAtIndex(int index, int val) {
        // 在指定下标位置插入，遍历到那个位置修改即可
        if (index < 0 || index > size) {
            return;
        }
        ListNode temp = head;
        // 拿到这个下标对应元素的前一个
        for (int i = 0; i <= index - 1; i++) {
            temp = temp.next;
        }
        ListNode next = temp.next;
        ListNode newNode = new ListNode(val);
        temp.next = newNode;
        newNode.next = next;
        size++;
    }

    public void deleteAtIndex(int index) {
        if (index < 0 || index >= size) {
            return;
        }
        ListNode temp = head;
        // 遍历到前一个，修改前一个的next
        for (int i = 0; i < index; i++) {
            temp = temp.next;
        }
        temp.next = temp.next.next;
        size--;
    }
}

/**
 * Your MyLinkedList object will be instantiated and called as such:
 * MyLinkedList obj = new MyLinkedList();
 * int param_1 = obj.get(index);
 * obj.addAtHead(val);
 * obj.addAtTail(val);
 * obj.addAtIndex(index,val);
 * obj.deleteAtIndex(index);
 */

反转链表

206. 反转链表

206. 反转链表 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * Definition for singly-linked list.
 * public class ListNode {
 * int val;
 * ListNode next;
 * ListNode() {}
 * ListNode(int val) { this.val = val; }
 * ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode last = null;
        while (head != null) {
            ListNode next = head.next;
            head.next = last;
            last = head;
            head = next;
        }
        return last;
    }
}

两两交换链表中的节点

24. 两两交换链表中的节点

24. 两两交换链表中的节点 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * Definition for singly-linked list.
 * public class ListNode {
 * int val;
 * ListNode next;
 * ListNode() {}
 * ListNode(int val) { this.val = val; }
 * ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode swapPairs(ListNode head) {
        ListNode newHead = new ListNode(-1, head);
        ListNode temp = newHead;
        while (temp.next != null && temp.next.next != null) {
            ListNode node1 = temp.next;
            ListNode node2 = temp.next.next;
            temp.next = node2;
            // 这里先调整node1的下一个为node2.next，下面再修改他就不受影响
            node1.next = node2.next;
            node2.next = node1;
            temp = node1;
        }
        return newHead.next;
    }
}

删除链表的倒数第N个节点

19. 删除链表的倒数第 N 个结点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/**
 * Definition for singly-linked list.
 * public class ListNode {
 * int val;
 * ListNode next;
 * ListNode() {}
 * ListNode(int val) { this.val = val; }
 * ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        if (n < 1 || head == null) {
            return head;
        }
        // 快慢指针
        ListNode newHead = new ListNode(-1, head);
        ListNode fast = newHead, slow = newHead;
        int i = 0;
        // 快指针先动n
        while (fast.next != null) {
            if (i == n) {
                break;
            }
            fast = fast.next;
            i++;
        }
        // 不够删
        if (i != n) {
            return newHead.next;
        }
        // 快慢指针一起动。知道快指针到尾部
        while (fast.next != null) {
            fast = fast.next;
            slow = slow.next;
        }
        // 这时候slow在要删除的上一个
        slow.next = slow.next.next;
        return newHead.next;
    }
}

链表相交

面试题 02.07. 链表相交

面试题 02.07. 链表相交 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * Definition for singly-linked list.
 * public class ListNode {
 * int val;
 * ListNode next;
 * ListNode(int x) {
 * val = x;
 * next = null;
 * }
 * }
 */
public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        if (headA == null || headB == null) {
            return null;
        }
        // 双指针，以不重叠的部分来看，交换去走的话，a走完a去b，b走完b去a，最后会碰在交点
        ListNode A = headA, B = headB;
        while (A != B) {
            A = A == null ? headB : A.next;
            B = B == null ? headA : B.next;
        }
        return A;
    }
}

环形链表II

142. 环形链表 II

[142. 环形链表 II - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 * Definition for singly-linked list.
 * class ListNode {
 * int val;
 * ListNode next;
 * ListNode(int x) {
 * val = x;
 * next = null;
 * }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {
        // 快慢指针
        ListNode slow = head, fast = head;
        while (fast != null && fast.next != null) {
            // 这里看有没有环，有环最后循环会有相等的位置，快的绕圈包住慢的，但不一定就是入口
            slow = slow.next;
            fast = fast.next.next;
            if (slow == fast) {
                // 有环，下面就需要找到入口位置,两个指针，从头结点和相遇结点，各走一步，直到相遇，相遇点即为环入口
                ListNode node1 = head, node2 = slow;
                while (node1 != node2) {
                    node1 = node1.next;
                    node2 = node2.next;
                }
                return node1;
            }
        }
        return null;
    }
}

哈希表

一般来说哈希表都是用来快速判断一个元素是否出现集合里。

对于哈希表，要知道哈希函数和哈希碰撞在哈希表中的作用。

哈希函数是把传入的key映射到符号表的索引上。

哈希碰撞处理有多个key映射到相同索引上时的情景，处理碰撞的普遍方式是拉链法和线性探测法。

接下来是常见的三种哈希结构：

  • 数组
  • set（集合）
  • map（映射）

当我们遇到了要快速判断一个元素是否出现集合里的时候，就要考虑哈希法。

但是哈希法也是牺牲了空间换取了时间，因为我们要使用额外的数组，set或者是map来存放数据，才能实现快速的查找。

如果在做面试题目的时候遇到需要判断一个元素是否出现过的场景也应该第一时间想到哈希法！

数组作为哈希表

242. 有效的字母异位词

242. 有效的字母异位词 - 力扣（LeetCode）

时间复杂度和空间复杂度太高，看下面方法，感觉被局限住了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public boolean isAnagram(String s, String t) {
        HashMap<Character, Integer> map = new HashMap<>();

        for (int i = 0; i < s.length(); i++) {
            map.put(s.charAt(i), map.getOrDefault(s.charAt(i), 0) + 1);
        }

        for (int i = 0; i < t.length(); i++) {
            if (map.getOrDefault(t.charAt(i), 0) == 0) {
                return false;
            } else {
                map.put(t.charAt(i), map.get(t.charAt(i)) - 1);
                if (map.get(t.charAt(i)) == 0) {
                    map.remove(t.charAt(i));
                }
            }
        }

        if (map.keySet().size() != 0) {
            return false;
        }

        return true;
    }
}

看下面

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public boolean isAnagram(String s, String t) {

        if (s.length() != t.length()) {
            return false;
        }

        int[] temp = new int[26];

        for (int i = 0; i < s.length(); i++) {
            temp[s.charAt(i) - 'a']++;
        }

        for (int i = 0; i < t.length(); i++) {
            temp[t.charAt(i) - 'a']--;
        }

        for (int i = 0; i < temp.length; i++) {
            if (temp[i] != 0) {
                return false;
            }
        }

        return true;
    }
}

383. 赎金信

383. 赎金信

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public boolean canConstruct(String ransomNote, String magazine) {

        int[] hash = new int[26];

        for (char c : magazine.toCharArray()) {
            hash[c - 'a'] += 1;
        }

        for (char c : ransomNote.toCharArray()) {
            hash[c - 'a'] -= 1;
        }

        for (int i : hash) {
            if (i < 0) {
                // 不够用
                return false;
            }
        }

        return true;
    }
}

当然可以HashMap解决，但是这里单用字符的26个的特性解决更好，不然HashMap维护红黑树很花时间并且占用内存更多

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public boolean canConstruct(String ransomNote, String magazine) {
        if (ransomNote.length() > magazine.length()) {
            return false;
        }
        HashMap<Character, Integer> map = new HashMap<>();
        // 将能使用的所有元素个数放到哈希表
        for (int i = 0; i < magazine.length(); i++) {
            map.put(magazine.charAt(i), map.getOrDefault(magazine.charAt(i), 0) + 1);
        }
        for (int i = 0; i < ransomNote.length(); i++) {
            int count = map.getOrDefault(ransomNote.charAt(i), 0);
            if (count > 0) {
                map.put(ransomNote.charAt(i), count - 1);
            } else {
                return false;
            }
        }
        return true;
    }
}

Set作为哈希表

349. 两个数组的交集

349. 两个数组的交集 - 力扣（LeetCode）

下面感觉是根据数据长度跟上面的字母一样可以取巧

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public int[] intersection(int[] nums1, int[] nums2) {
        // 可以用长度1001的数组保存即可，因为范围就0到1000，最后看数量相等就行
        int[] hash1 = new int[1001];
        int[] hash2 = new int[1001];
        for (int i = 0; i < nums1.length; i++) {
            hash1[nums1[i]]++;
        }
        for (int i = 0; i < nums2.length; i++) {
            hash2[nums2[i]]++;
        }
        int size = 0;
        for (int i = 0; i < hash1.length; i++) {
            int count = hash1[i] > hash2[i] ? hash2[i] : hash1[i];
            if (count != 0) {
                size++;
            }
        }
        int[] result = new int[size];
        int k = 0;
        for (int i = 0; i < hash1.length; i++) {
            int count = hash1[i] > hash2[i] ? hash2[i] : hash1[i];
            if (count != 0) {
                result[k++] = i;
            }
        }
        return result;
    }
}

HashSet解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int[] intersection(int[] nums1, int[] nums2) {
        if (nums1.length == 0 || nums2.length == 0) {
            return new int[0];
        }
        // HashSet解决
        Set<Integer> set = new HashSet<>();
        Set<Integer> set2 = new HashSet<>();
        for (int i = 0; i < nums1.length; i++) {
            set.add(nums1[i]);
        }
        for (int i = 0; i < nums2.length; i++) {
            if (set.contains(nums2[i])) {
                set2.add(nums2[i]);
            }
        }
        int[] result = new int[set2.size()];
        int t = 0;
        for (int i : set2) {
            result[t++] = i;
        }
        return result;
    }
}

Map作为哈希表

1. 两数之和

1. 两数之和 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int[] twoSum(int[] nums, int target) {
        // 两次遍历时间复杂度On^2了，可以排序后双指针，但代码复杂了，这里用哈希
        HashMap<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < nums.length; i++) {
            int temp = target - nums[i];
            if (map.containsKey(temp)) {
                return new int[] { i, map.get(temp) };
            } else {
                map.put(nums[i], i);
            }
        }
        return null;
    }
}

454. 四数相加 II

454. 四数相加 II - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
        int count = 0;
        HashMap<Integer,Integer>map = new HashMap<>();
        //先处理前面两个数字，就同两数两加了
        for(int i :nums1){
            for(int j :nums2){
                map.put(i+j,map.getOrDefault(i+j,0)+1);
            }
        }
        //再处理后面两个数组
          for(int i :nums3){
            for(int j :nums4){
                count += map.getOrDefault(0-i-j,0);
            }
        }
        return count;
    }
}

双指针求多数和

15. 三数之和

两数之和 就不能使用双指针法，因为1.两数之和 (opens new window)要求返回的是索引下标， 而双指针法一定要排序，一旦排序之后原数组的索引就被改变了。如果1.两数之和 (opens new window)要求返回的是数值的话，就可以使用双指针法了。

15. 三数之和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();
        // 先对nums进行排序
        Arrays.sort(nums);
        // 外层循环，控制第一个数字
        for (int i = 0; i < nums.length; i++) {
            // 去重，第一个数字都大没必要比了
            if (nums[i] > 0) {
                break;
            }
            // 对第一个数字去重，跟i-1比较合适，跟i+1比较不合适，因为i+1跟i相等就去除掉，那么如果一个数组为-1，-1,2就没机会了，应该让第二次相等的去掉
            if (i > 0 && nums[i] == nums[i - 1]) {
                continue;
            }
            // 内层循环控制第二和第三个数字，内层就是双指针了
            int right = nums.length - 1;
            int left = i + 1;
            while (left < right) {
                if (nums[left] + nums[right] + nums[i] < 0) {
                    // 太小了，移动left变大
                    left++;
                } else if (nums[left] + nums[right] + nums[i] > 0) {
                    // 太大了，移动right变小
                    right--;
                } else {
                    // 相等
                    result.add(Arrays.asList(nums[i], nums[left], nums[right]));
                    // 找到第一个后再去重，跟上一个和下一个去重都可以，注意left++和right--和去重的顺序就行，保证最后的left和right是新的不为用过的就行，这里跟上面一样吧，跟上一个用过的去重
                    left++;
                    right--;
                    while (left < right && nums[left] == nums[left - 1]) {
                        left++;
                    }
                    while (left < right && nums[right] == nums[right + 1]) {
                        right--;
                    }
                 
                }
            }
        }
        return result;
    }
}

18. 四数之和

18. 四数之和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
class Solution {
    public List<List<Integer>> fourSum(int[] nums, int target) {
        // 前面的三数之和和这里的四数之和都是为了减少一层循环而出现的方法,看完这两个就可以发现规律了，5数，6数和都一样了
        List<List<Integer>> result = new ArrayList<>();
        // 先排序
        Arrays.sort(nums);
        // 控制第一个数字
        for (int i = 0; i < nums.length; i++) {

            // 第一级剪枝，三数之和要求和是0并且排序过，只要第一个大于0就没机会了，这里不一样
            if (nums[i] >= 0 && nums[i] > target) {
                break;
            }

            // 去重,同三数之和，跟前一个比较
            if (i > 0 && nums[i] == nums[i - 1]) {
                continue;
            }

            // 控制第二个数字
            for (int j = i + 1; j < nums.length; j++) {

                // 第二级减枝
                if (nums[i] + nums[j] >= 0 && nums[i] + nums[j] > target) {
                    break;
                }

                // 去重
                if (j > i + 1 && nums[j] == nums[j - 1]) {
                    continue;
                }

                // 内重循环，双指针
                int left = j + 1;
                int right = nums.length - 1;
                while (left < right) {
                    long sum = (long) nums[i] + nums[j] + nums[left] + nums[right];
                    if (sum < target) {
                        // 当前组合太小了，left右移
                        left++;
                    } else if (sum > target) {
                        // 当前组合超了，right左移，减小和
                        right--;
                    } else {
                        // 相等
                        result.add(Arrays.asList(nums[i], nums[j], nums[left], nums[right]));
                        // 两指针收缩
                        left++;
                        right--;
                        // 收缩后需要去重，看是不是之前重复过的数字
                        while (left < right && nums[left] == nums[left - 1]) {
                            left++;
                        }
                        while (left < right && nums[right] == nums[right + 1]) {
                            right--;
                        }
                    }
                }
            }

        }

        return result;
    }
}

字符串

344. 反转字符串

344. 反转字符串

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public void reverseString(char[] s) {
        //双指针，其实就是沿着中线左右互换，从两头开始不断交换
        int left = 0,right = s.length-1;
        while(left<right){
            char temp = s[left];
            s[left] = s[right];
            s[right] = temp;
            left++;
            right--;
        }
    }
}

541. 反转字符串 II

541. 反转字符串 II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    public String reverseStr(String s, int k) {
        char[] target = s.toCharArray();
        int count = target.length / (2 * k);
        for (int i = 0; i < count; i++) {
            reverse(target, 2 * k * i, 2 * k * i + k - 1);
        }
        // 看剩余多少
        int balance = target.length % (2 * k);
        if (balance >= k) {
            reverse(target, target.length - balance, target.length - balance + k - 1);
        } else if (balance != 0) {
            reverse(target, target.length - balance, target.length - 1);
        }
        return new String(target);
    }

    public void reverse(char[] target, int left, int right) {
        while (left < right) {
            char c = target[left];
            target[left] = target[right];
            target[right] = c;
            left++;
            right--;
        }
    }
}

151. 反转字符串中的单词

151. 反转字符串中的单词

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public String reverseWords(String s) {
        // 去除头尾空格
        String target = s.trim();
        // 保存答案
        StringBuilder builder = new StringBuilder();
        // 双指针
        int right = target.length(), left = target.length() - 1;
        while (left >= 0) {
            if (left - 1 >= 0 && target.charAt(left - 1) != ' ') {
                left--;
            } else {
                // 遇到空格了或者到顶了
                builder.append(target.substring(left, right));
                builder.append(" ");
                // 跳过前面的空格
                left--;
                while (left >= 0 && target.charAt(left) == ' ') {
                    left--;
                }
                right = left + 1;
            }
        }

        // 去除尾部空格
        return builder.toString().trim();
    }
}

JZ58 左旋转字符串

左旋转字符串_牛客题霸_牛客网 (nowcoder.com)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param str string字符串 
     * @param n int整型 
     * @return string字符串
     */
    public String LeftRotateString (String str, int n) {
        if(str.isEmpty()){
            return "";
        }
        //实际需要移动的位数
        int real = n % str.length();
        char[] result = new char[str.length()];
        int index = 0;
        for(int i = real;i<str.length();i++){
            result[index++] = str.charAt(i);
        }
        for(int i = 0;i<real;i++){
            result[index++] = str.charAt(i);
        }
        return new String(result);
    }
}

28. 找出字符串中第一个匹配项的下标

28. 找出字符串中第一个匹配项的下标

简单实现，看下面高级的KMP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int strStr(String haystack, String needle) {
        int length1 = haystack.length(), length2 = needle.length();
        // 双指针
        int left = 0;
        while (length1 - left >= length2) {
            if (haystack.substring(left, left + length2).equals(needle)) {
                return left;
            }
            left++;
        }
        return -1;
    }
}

KMP实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution {
    public int strStr(String haystack, String needle) {
        // KMP实现
        int[] next = new int[needle.length()];
        getNext(next, needle);
        int j = 0;
        for (int i = 0; i < haystack.length(); i++) {
            // 不断回退
            while (j > 0 && haystack.charAt(i) != needle.charAt(j)) {
                j = next[j - 1];
            }
            if (haystack.charAt(i) == needle.charAt(j)) {
                j++;
            }
            // j为前缀和
            if (j == needle.length()) {
                return i - needle.length() + 1;
            }
        }
        return -1;
    }

    // 求next数组（前缀表），这里不做特殊处理，就让next数组跟前缀表完全一样
    public void getNext(int[] next, String str) {
        // 初始化，i表示后缀的末尾位置（代表后缀），j代表当前匹配的最长相同前后缀的长度（代表前缀），也可以看作是前缀的末尾索引加一
        int j = 0;
        // 0没有前后缀，初始化为0
        next[0] = 0;
        // 0已经初始化过了，i从1开始
        for (int i = 1; i < str.length(); i++) {
            // 如果i和j不等就要回退，避免重复比较
            while (j > 0 && str.charAt(i) != str.charAt(j)) {
                j = next[j - 1];
            }
            if (str.charAt(i) == str.charAt(j)) {
                // 前后缀相等就从这个位置的下一个匹配
                j++;
            }
            // 更新前缀表
            next[i] = j;
        }
    }
}

459. 重复的子字符串

459. 重复的子字符串

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public boolean repeatedSubstringPattern(String s) {
        //KMP实现,具体证明看代码随想录吧
        int j = 0;
        int[] next = new int[s.length()];
        //求next数组
        for(int i = 1;i<s.length();i++){
            while(j>0&&s.charAt(i)!=s.charAt(j)){
                j = next[j-1];
            }
            if(s.charAt(i)==s.charAt(j)){
                j++;
            }
            next[i] = j;
        }
        if(next[s.length()-1]>0&&s.length()%(s.length()-next[s.length()-1])==0){
            return true;
        }
        return false;
    }
}

KMP算法

解决字符串匹配的问题

文本串是原本的字符串，模式串是否在文本串中出现过

帮你把KMP算法学个通透！（理论篇）_哔哩哔哩_bilibili

帮你把KMP算法学个通透！（求next数组代码篇）_哔哩哔哩_bilibili

前缀：一个字符串包含首字母但不包含尾字母之间的字符串的所有子序列

image-20241013224126054

后缀： 一个字符串包含尾字母但不包含首字母之间的字符串的所有子序列

image-20241013224156668

这里要求最长相等的前缀的后缀的长度（网上很多用的是求公共前后缀），这个最后求出来就是前缀表

image-20241013224107355

如何使用前缀表进行匹配？

出现了一个位置不匹配了，那这时候可以看前面字符串的最长相等前后缀的长度，这个长度就是继续匹配的下标

image-20241013224717362

某些代码用的next数组或者prefix数组，其实就是前缀表，但是next数组可能是经过一些调整的，如右移或者统一减一，这个是涉及到KMP算法的具体实现的过程的，就算用原封不动的前缀表作为next数组也可以完成我们的操作

具体算法的实现

  1. 初始化next数组和函数各个变量

    i指向后缀的末尾位置，j指向前缀的末尾位置，j初始化为0，next[0]=0，0下标自然回退到0开始比较，那i呢？i的话是在遍历中进行的，一开始要从1开始才能比较，从0开始就重叠了，没有前后缀了，不满足i和j的定义

  2. 处理前后缀不相同的情况

    image-20241013231137522

  3. 处理前后缀相同的情况

    image-20241013231411289

  4. 更新next数组的值

栈和队列

Java精讲 | 45张图庖丁解牛18种Queue，你知道几种？-腾讯云开发者社区-腾讯云 (tencent.com)

Stack详解（Java实现方式）_java stack-CSDN博客

互相模拟

232. 用栈实现队列

232. 用栈实现队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class MyQueue {

    Stack<Integer> stack1 = new Stack<>();
    Stack<Integer> stack2 = new Stack<>();

    public MyQueue() {

    }

    public void push(int x) {
        // stack2的内容全会stack1先
        while (!stack2.isEmpty()) {
            stack1.push(stack2.pop());
        }
        // 先放入1，再进入2就是正序了
        stack1.push(x);
        while (!stack1.isEmpty()) {
            stack2.push(stack1.pop());
        }
    }

    public int pop() {
        if (stack2.isEmpty()) {
            return -1;
        }
        return stack2.pop();
    }

    public int peek() {
        if (stack2.isEmpty()) {
            return -1;
        }
        return stack2.peek();
    }

    public boolean empty() {
        return stack2.isEmpty();
    }
}

/**
 * Your MyQueue object will be instantiated and called as such:
 * MyQueue obj = new MyQueue();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.peek();
 * boolean param_4 = obj.empty();
 */

225. 用队列实现栈

225. 用队列实现栈

注意top的部分，在while里面移动完再判断size是否等于1赋值有问题的，长度刚好为1，移动完再判断就对不上了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
class MyStack {

    Queue<Integer> queue1 = new ArrayDeque<>();
    Queue<Integer> queue2 = new ArrayDeque<>();

    public MyStack() {

    }

    public void push(int x) {
        queue1.offer(x);
    }

    public int pop() {
        if (queue1.size() < 1) {
            return -1;
        }
        // 移动queue1中的东西到queue2知道只剩一个pop即可
        while (queue1.size() > 1) {
            queue2.offer(queue1.poll());
        }
        // queue2的再放回queue1
        while (!queue2.isEmpty()) {
            queue1.offer(queue2.poll());
        }
        return queue1.poll();
    }

    public int top() {
        if (queue1.size() < 1) {
            return -1;
        }
        // 移动queue1中的东西到queue2知道只剩一个pop即可
        while (queue1.size() > 1) {
            queue2.offer(queue1.poll());
        }
        int result = queue1.peek();
        queue2.offer(queue1.poll());
        // queue2的再放回queue1
        while (!queue2.isEmpty()) {
            queue1.offer(queue2.poll());
        }
        return result;
    }

    public boolean empty() {
        return queue1.isEmpty();
    }
}

/**
 * Your MyStack object will be instantiated and called as such:
 * MyStack obj = new MyStack();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.top();
 * boolean param_4 = obj.empty();
 */

栈使用

20. 有效的括号

20. 有效的括号

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public boolean isValid(String s) {
        Stack<Character> stack = new Stack<>();
        for (int i = 0; i < s.length(); i++) {
            char c = s.charAt(i);
            if (c == '(' || c == '[' || c == '{') {
                stack.push(c);
            } else {
                if (stack.isEmpty()) {
                    return false;
                }
                char temp = stack.pop();
                if (!((c == ')' && temp == '(') || (c == ']' && temp == '[') || (c == '}' && temp == '{'))) {
                    return false;
                }
            }
        }
        if (stack.isEmpty()) {
            return true;
        }
        return false;
    }
}

1047. 删除字符串中的所有相邻重复项

1047. 删除字符串中的所有相邻重复项

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public String removeDuplicates(String s) {
        Stack<Character> stack = new Stack<>();
        for (int i = 0; i < s.length(); i++) {
            char c = s.charAt(i);
            if (stack.isEmpty() || stack.peek() != c) {
                stack.push(c);
            } else {
                stack.pop();
            }
        }
        //stack先进后出，倒序放出来才是正的
        char[] result = new char[stack.size()];
        int i = result.length - 1;
        while (!stack.isEmpty()) {
            result[i--] = stack.pop();
        }
        return new String(result);
    }
}

拿字符串直接作为栈，省去了栈还要转为字符串的操作。另外思路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public String removeDuplicates(String s) {
        // 将 res 当做栈
        // 也可以用 StringBuilder 来修改字符串，速度更快
        // StringBuilder res = new StringBuilder();
        StringBuffer res = new StringBuffer();
        // top为 res 的长度
        int top = -1;
        for (int i = 0; i < s.length(); i++) {
            char c = s.charAt(i);
            // 当 top > 0,即栈中有字符时，当前字符如果和栈中字符相等，弹出栈顶字符，同时 top--
            if (top >= 0 && res.charAt(top) == c) {
                res.deleteCharAt(top);
                top--;
            // 否则，将该字符 入栈，同时top++
            } else {
                res.append(c);
                top++;
            }
        }
        return res.toString();
    }
}

150. 逆波兰表达式求值

150. 逆波兰表达式求值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    public int evalRPN(String[] tokens) {
        Stack<Integer> stack = new Stack<>();

        for (int i = 0; i < tokens.length; i++) {
            String temp = tokens[i];
            if (temp.equals("+") || temp.equals("-") || temp.equals("*") || temp.equals("/")) {
                // 为特殊符号需要去除两个数
                int second = stack.pop();
                int first = stack.pop();
                if (temp.equals("+")) {
                    stack.push(first + second);
                } else if (temp.equals("-")) {
                    stack.push(first - second);
                } else if (temp.equals("*")) {
                    stack.push(first * second);
                } else if (temp.equals("/")) {
                    stack.push(first / second);
                }
            } else {
                stack.push(Integer.valueOf(temp));
            }
        }

        return stack.pop();
    }
}

代码随想录给的用Deque，双向队列来的，既可以做队列也可做栈使用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int evalRPN(String[] tokens) {
        Deque<Integer> stack = new LinkedList();
        for (String s : tokens) {
            if ("+".equals(s)) {        // leetcode 内置jdk的问题，不能使用==判断字符串是否相等
                stack.push(stack.pop() + stack.pop());      // 注意 - 和/ 需要特殊处理
            } else if ("-".equals(s)) {
                stack.push(-stack.pop() + stack.pop());
            } else if ("*".equals(s)) {
                stack.push(stack.pop() * stack.pop());
            } else if ("/".equals(s)) {
                int temp1 = stack.pop();
                int temp2 = stack.pop();
                stack.push(temp2 / temp1);
            } else {
                stack.push(Integer.valueOf(s));
            }
        }
        return stack.pop();
    }
}

单调栈

通常是一维数组，要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置，此时我们就要想到可以用单调栈了。时间复杂度为O(n)。

单调栈的本质是空间换时间，因为在遍历的过程中需要用一个栈来记录右边第一个比当前元素高的元素，优点是整个数组只需要遍历一次。

更直白来说，就是用一个栈来记录我们遍历过的元素，因为我们遍历数组的时候，我们不知道之前都遍历了哪些元素，以至于遍历一个元素找不到是不是之前遍历过一个更小的，所以我们需要用一个容器（这里用单调栈）来记录我们遍历过的元素。

在使用单调栈的时候首先要明确如下几点：

  1. 单调栈里存放的元素是什么？

单调栈里只需要存放元素的下标i就可以了，如果需要使用对应的元素，直接T[i]就可以获取。

  1. 单调栈里元素是递增呢？ 还是递减呢？

注意使用的是栈，是先进后出的，别懵逼了，后面没睡醒一样，当成队列一直觉得有问题，笑死

739. 每日温度

739. 每日温度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int[] dailyTemperatures(int[] temperatures) {
        int[] result = new int[temperatures.length];
        // 单调栈存放的是下标
        Deque<Integer> stack = new LinkedList<>();
        for (int i = 0; i < temperatures.length; i++) {
            // 当一个元素比栈顶元素大的时候就可以逐渐抛出并根据下标计算新的出现的位置了，所以才需要存储的是下标
            while (!stack.isEmpty() && temperatures[i] > temperatures[stack.peek()]) {
                result[stack.peek()] = i - stack.peek();
                stack.pop();
            }
            stack.push(i);
        }
        return result;
    }
}

496. 下一个更大元素 I

496. 下一个更大元素 I

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public int[] nextGreaterElement(int[] nums1, int[] nums2) {
        int[] result = new int[nums1.length];
        // 全填充为-1先
        Arrays.fill(result, -1);
        // Map记录值和下标
        HashMap<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < nums1.length; i++) {
            map.put(nums1[i], i);
        }
        // 单调栈保存下标
        Stack<Integer> stack = new Stack<>();
        for (int i = 0; i < nums2.length; i++) {
            while (!stack.isEmpty() && nums2[i] > nums2[stack.peek()]) {
                // 抛出的就是需要检查nums1有没有的
                int temp = nums2[stack.pop()];
                if (map.containsKey(temp)) {
                    result[map.get(temp)] = nums2[i];
                }
            }
            stack.push(i);
        }
        return result;
    }
}

503. 下一个更大元素 II

503. 下一个更大元素 II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int[] nextGreaterElements(int[] nums) {
        //这里确实很技巧，循环其实使用单调栈的话回到自己就完成循环了，也就是拼接两个数组就可以了，直接遍历两边就好
        int[] result = new int[nums.length];
        Arrays.fill(result,-1);
        Stack<Integer>stak = new Stack<>();
        //套娃两圈
        for(int i = 0;i<2*nums.length;i++){
            //取模保证不越界
            while(!stak.isEmpty()&&nums[i%nums.length]>nums[stak.peek()]){
                int temp = stak.pop();
                result[temp] = nums[i%nums.length];
            }
            stak.push(i%nums.length);
        }
        return result;
    }
}

42. 接雨水

42. 接雨水

这题可以双指针解决的，这个是双指针优化版本，还可以遍历两边，分别把从左往右走的左边柱子最大值记录下俩，从右往左走的最大值记录下来，之后再遍历求和即可，如下

1
2
int count = Math.min(maxLeft[i], maxRight[i]) - height[i];
if (count > 0) sum += count;

双指针优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
    public int trap(int[] height) {
        // 高度数组过短时无法存水
        if (height.length <= 2) {
            return 0;
        }

        // 左右指针分别从两侧开始
        int left = 1, right = height.length - 2;
        // 初始化左右最大值为边界值
        int maxLeft = height[0], maxRight = height[height.length - 1];
        // 用于累积结果的变量
        int result = 0;

        // 当左指针不超过右指针时继续计算
        while (left <= right) {
            // 更新左右最大值
            maxLeft = Math.max(maxLeft, height[left]);
            maxRight = Math.max(maxRight, height[right]);

            // 根据较小的最大值决定移动方向
            if (maxLeft < maxRight) {
                // 左侧较低，计算左边能存多少水
                result += maxLeft - height[left];
                left++;
            } else {
                // 右侧较低，计算右边能存多少水
                result += maxRight - height[right];
                right--;
            }
        }

        return result;
    }
}

单调栈（找每个柱子左右两边第一个大于该柱子高度的柱子）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    public int trap(int[] height) {
        if(height.length<=2){
            return 0;
        }
        //单调栈解法，先进后出
        int result = 0;
        //保存下标即可
        Stack<Integer>stack = new Stack<>();
        for(int  i = 0;i<height.length;i++){
            //栈为空直接丢进去，不为空并且比栈顶的高，也就是栈内都是单调增的
            while(!stack.isEmpty()&&height[i]>height[stack.peek()]){
                int mid = stack.pop();
                if(!stack.isEmpty()){
                    //丢出的一个视为中间的凹槽的值，丢出一个后栈内还有才能说明能接水，不然就两个接不了水
                    int left = stack.peek();
                    //计算接水面积
                    //高度差
                    int h = Math.min(height[left],height[i]) - height[mid];
                    //宽度
                    int w = i - left - 1;
                    //面积
                    result += h * w;
                }
            }
            stack.push(i);
        }
        return result;

    }
}

84. 柱状图中最大的矩形

84. 柱状图中最大的矩形

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int largestRectangleArea(int[] heights) {
        // 单调栈，这里头尾都加0是为了简化代码逻辑，不需要手动处理特殊情况，如[2, 1, 5, 6, 2, 3]，最后不加0就需要自己处理剩余情况
        int[] nums = new int[heights.length + 2];
        System.arraycopy(heights, 0, nums, 1, heights.length);
        int result = 0;
        // 0先入栈
        Stack<Integer> stack = new Stack<>();
        stack.push(0);
        for (int i = 1; i < nums.length; i++) {
            while (nums[i] < nums[stack.peek()]) {
                // 找第一个比目标值小的柱子
                int mid = stack.pop();
                int left = stack.peek();
                int w = i - left - 1;
                result = Math.max(result, w * nums[mid]);
            }
            stack.push(i);
        }
        return result;
    }
}

队列使用

239. 滑动窗口最大值

239. 滑动窗口最大值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        // 大顶堆不能直接删除某个值，这里使用大顶堆不合适
        int[] result = new int[nums.length - k + 1];
        // 手动借助双端队列维护一个可能成为最大值的队列并且单调队列即可，保存下标即可
        Deque<Integer> queue = new ArrayDeque<>();
        for (int i = 0; i < nums.length; i++) {

            // 1.队列头结点需要在[i - k + 1, i]范围内，不符合则要弹出
            while (!queue.isEmpty() && queue.peekFirst() < i - k + 1) {
                queue.pollFirst();
            }

            // 2.既然是单调，就要保证每次放进去的数字要比末尾的都大，否则也弹出
            while (!queue.isEmpty() && nums[queue.peekLast()] < nums[i]) {
                queue.pollLast();
            }

            // 到这里就可以放入了
            queue.offerLast(i);

            // 滑动窗口产生了，直接从队列头去拿即可
            if (i >= k - 1) {
                result[i - k + 1] = nums[queue.peekFirst()];
            }
        }
        return result;
    }
}

结合使用

347. 前 K 个高频元素

347. 前 K 个高频元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        // 统计每个元素出现的频率
        HashMap<Integer, Integer> map = new HashMap<>();
        for (int num : nums) {
            map.put(num, map.getOrDefault(num, 0) + 1);
        }

        // 小顶堆，按照频率排序
        PriorityQueue<Map.Entry<Integer, Integer>> queue = new PriorityQueue<>(
            (a, b) -> a.getValue() - b.getValue()
        );

        // 遍历map，维护大小为k的小顶堆
        for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
            queue.offer(entry);
            if (queue.size() > k) {
                queue.poll(); // 如果堆的大小超过k，就弹出堆顶（频率最小的元素）
            }
        }

        // 从堆中取出前k个高频元素
        int[] result = new int[k];
        int i = 0;
        while (!queue.isEmpty()) {
            result[i++] = queue.poll().getKey(); // 提取元素而不是频率
        }

        return result;
    }
}

二叉树

种类直接去这里看吧

代码随想录 (programmercarl.com)

二叉树的遍历方式

递归

这里帮助大家确定下来递归算法的三个要素。每次写递归，都按照这三要素来写，可以保证大家写出正确的递归算法！

  1. 确定递归函数的参数和返回值： 确定哪些参数是递归的过程中需要处理的，那么就在递归函数里加上这个参数， 并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型。
  2. 确定终止条件： 写完了递归算法, 运行的时候，经常会遇到栈溢出的错误，就是没写终止条件或者终止条件写的不对，操作系统也是用一个栈的结构来保存每一层递归的信息，如果递归没有终止，操作系统的内存栈必然就会溢出。
  3. 确定单层递归的逻辑： 确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程。

144. 二叉树的前序遍历

144. 二叉树的前序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {

    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        preorder(root, result);
        return result;
    }

    public void preorder(TreeNode node, List<Integer> result) {
        if (node == null) {
            return;
        }
        // 中
        result.add(node.val);
        // 左
        preorder(node.left, result);
        // 右
        preorder(node.right, result);
    }
}

94. 二叉树的中序遍历

94. 二叉树的中序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        inorder(root, result);
        return result;
    }

    public void inorder(TreeNode root, List<Integer> result) {
        if (root == null) {
            return;
        }
        // 左
        inorder(root.left, result);
        // 中
        result.add(root.val);
        // 右
        inorder(root.right, result);
    }
}

145. 二叉树的后序遍历

145. 二叉树的后序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        postorder(root, result);
        return result;
    }

    public void postorder(TreeNode root, List<Integer> result) {
        if (root == null) {
            return;
        }
        // 左
        postorder(root.left, result);
        // 右
        postorder(root.right, result);
        // 中
        result.add(root.val);
    }
}

589. N 叉树的前序遍历

589. N 叉树的前序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {

    List<Integer>result = new ArrayList<>();

    public List<Integer> preorder(Node root) {
        pre(root);
        return result;
    }

    public void pre(Node node){
        if(node==null){
            return;
        }
        result.add(node.val);
        //按顺序遍历子节点
        if(node.children!=null&&!node.children.isEmpty()){
            for(Node n:node.children){
                pre(n);
            }
        }
    }
}

590. N 叉树的后序遍历

590. N 叉树的后序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {

    List<Integer> result = new ArrayList<>();

    public List<Integer> postorder(Node root) {
        post(root);
        return result;
    }

    public void post(Node node) {
        if (node == null) {
            return;
        }
        if (node.children != null && !node.children.isEmpty()) {
            for (Node n : node.children) {
                post(n);
            }
        }
        result.add(node.val);
    }
}

迭代

我还是习惯这种不统一的思路，虽然老忘记，统一风格直接看代码随想录官网的吧，代码随想录 (programmercarl.com)

144. 二叉树的前序遍历

144. 二叉树的前序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {

    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        // 先进后出，中间的直接输入，然后先进右再进左，左的处理后又放自己子树的，最后才回来右子树的
        Stack<TreeNode> stack = new Stack<>();
        if (root != null) {
            stack.push(root);
        }
        while (!stack.isEmpty()) {
            // 中
            TreeNode node = stack.pop();
            result.add(node.val);
            // 先右，后出右
            if (node.right != null) {
                stack.push(node.right);
            }
            // 后左，先出左
            if (node.left != null) {
                stack.push(node.left);
            }
        }
        return result;
    }
}

94. 二叉树的中序遍历

94. 二叉树的中序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
            List<Integer>result = new ArrayList<>();

            Stack<TreeNode>stack = new Stack<>();
            while(root!=null||!stack.isEmpty()){
                if(root!=null){
                    //要一直先往左边跑看有就放,直到左边没有
                    stack.push(root);
                    root = root.left;
                }else{
                    //走到这里说明左边没有了，可以放入这个值，然后到右子树
                    root = stack.pop();
                    result.add(root.val);
                    root = root.right;
                }
            }
            return result;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    public int getMinimumDifference(TreeNode root) {
        // 好就没写中序遍历了，怕忘记，这里写写吧,题目说了树不会为空
        // 结果
        int min = Integer.MAX_VALUE;
        // 保存上次访问的节点
        TreeNode last = null;
        Stack<TreeNode> stack = new Stack<>();
        while (root != null || !stack.isEmpty()) {
            // 一路向左
            if (root != null) {
                stack.push(root);
                root = root.left;
            } else {
                // 抛出处理中间的
                root = stack.pop();
                if (last != null) {
                    min = Math.min(min, root.val - last.val);
                }
                last = root;
                // 处理右边的
                root = root.right;
            }
        }
        return min;
    }
}

145. 二叉树的后序遍历

145. 二叉树的后序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        TreeNode pre = null;
        while (root != null || !stack.isEmpty()) {
            // 一路向左
            while (root != null) {
                stack.push(root);
                root = root.left;
            }
            // 先不抛出，处理才需要抛出
            root = stack.peek();
            // 看右边有没有处理过
            if (root.right == null || root.right == pre) {
                // 右边为空或者访问过，那么就可以输出
                result.add(root.val);
                // 抛出
                stack.pop();
                // 记录处理过
                pre = root;
                // 置空，防止重新又处理，之后重新拿右边的
                root = null;
            } else {
                // 没有处理过
                root = root.right;
            }
        }
        return result;
    }
}

另一种思路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// 后序遍历顺序 左-右-中 入栈顺序：中-左-右 出栈顺序：中-右-左， 最后翻转结果
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null){
            return result;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()){
            TreeNode node = stack.pop();
            result.add(node.val);
            if (node.left != null){
                stack.push(node.left);
            }
            if (node.right != null){
                stack.push(node.right);
            }
        }
        Collections.reverse(result);
        return result;
    }
}

层次遍历

102. 二叉树的层序遍历

102. 二叉树的层序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> result = new ArrayList<>();
        Queue<TreeNode> queue = new LinkedList<>();
        if (root != null) {
            queue.offer(root);
        }
        while (!queue.isEmpty()) {
            // 一层
            int size = queue.size();
            List<Integer>list = new ArrayList<>();
            while (size != 0) {
                size--;
                root = queue.poll();
                list.add(root.val);
                if (root.left != null) {
                    queue.offer(root.left);
                }
                if (root.right != null) {
                    queue.offer(root.right);
                }
            }
              result.add(list);
        }
        return result;
    }
}

107. 二叉树的层序遍历 II

107. 二叉树的层序遍历 II

就倒个序，挺无聊的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    public List<List<Integer>> levelOrderBottom(TreeNode root) {
        List<List<Integer>> result = new ArrayList<>();
        Queue<TreeNode> queue = new LinkedList<>();
        if (root != null) {
            queue.offer(root);
            while (!queue.isEmpty()) {
                int size = queue.size();
                List<Integer> list = new ArrayList<>();
                while (size != 0) {
                    size--;
                    root = queue.poll();
                    list.add(root.val);
                    if (root.left != null) {
                        queue.offer(root.left);
                    }
                    if (root.right != null) {
                        queue.offer(root.right);
                    }
                }
                //不用检查list数量，一定不为空才进循环
                result.add(0, list);
            }
        }
        return result;
    }
}

199. 二叉树的右视图

199. 二叉树的右视图

题目的意思是花好二叉树后直接从右边往左边看看到最外围的节点，从上往下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public List<Integer> rightSideView(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        Queue<TreeNode> queue = new LinkedList<>();
        if (root != null) {
            queue.offer(root);
            while (!queue.isEmpty()) {
                int size = queue.size();
                while (size > 0) {
                    root = queue.poll();
                    if (root.left != null) {
                        queue.offer(root.left);
                    }
                    if (root.right != null) {
                        queue.offer(root.right);
                    }
                    size--;
                }
                // 最后一个
                result.add(root.val);
            }
        }
        return result;
    }
}

637. 二叉树的层平均值

637. 二叉树的层平均值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    public List<Double> averageOfLevels(TreeNode root) {
        List<Double> result = new ArrayList<>();
        Queue<TreeNode> queue = new LinkedList<>();
        if (root != null) {
            queue.offer(root);
            while (!queue.isEmpty()) {
                int size = queue.size();
                int temp = size;
                double sum = 0.0;
                while (size > 0) {
                    root = queue.poll();
                    sum += root.val;
                    if (root.left != null) {
                        queue.offer(root.left);
                    }
                    if (root.right != null) {
                        queue.offer(root.right);
                    }
                    size--;
                }
                result.add(sum / temp);
            }
        }
        return result;
    }
}

429. N 叉树的层序遍历

429. N 叉树的层序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
    public List<List<Integer>> levelOrder(Node root) {
        List<List<Integer>> result = new ArrayList<>();
        if (root != null) {
            Queue<Node> queue = new LinkedList<>();
            queue.offer(root);
            while (!queue.isEmpty()) {
                int size = queue.size();
                List<Integer> list = new ArrayList<>();
                while (size != 0) {
                    Node node = queue.poll();
                    list.add(node.val);
                    //当前节点有子孩子才加入队列
                    if (node.children != null && !node.children.isEmpty()) {
                        for (Node n : node.children) {
                            queue.offer(n);
                        }
                    }
                    size--;
                }
                result.add(list);
            }
        }
        return result;
    }
}

515. 在每个树行中找最大值

515. 在每个树行中找最大值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 * int val;
 * TreeNode left;
 * TreeNode right;
 * TreeNode() {}
 * TreeNode(int val) { this.val = val; }
 * TreeNode(int val, TreeNode left, TreeNode right) {
 * this.val = val;
 * this.left = left;
 * this.right = right;
 * }
 * }
 */
class Solution {
    public List<Integer> largestValues(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root != null) {
            Queue<TreeNode> queue = new LinkedList<>();
            queue.offer(root);
            while (!queue.isEmpty()) {
                int size = queue.size();
                int temp = Integer.MIN_VALUE;
                while (size != 0) {
                    root = queue.poll();
                    temp = Math.max(temp, root.val);
                    if (root.left != null) {
                        queue.offer(root.left);
                    }
                    if (root.right != null) {
                        queue.offer(root.right);
                    }
                    size--;
                }
                result.add(temp);
            }
        }
        return result;
    }
}

116. 填充每个节点的下一个右侧节点指针

116. 填充每个节点的下一个右侧节点指针

别先抛出一个，易错

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
    public Node connect(Node root) {
        if (root == null) {
            return root;
        }
        
        Queue<Node> queue = new LinkedList<>();
        queue.offer(root);
        
        while (!queue.isEmpty()) {
            int size = queue.size(); 
            Node last = null; 
            
            for (int i = 0; i < size; i++) {
                Node current = queue.poll();
                
                // 连接上一个节点
                if (last != null) {
                    last.next = current;
                }
                
                last = current; 
                // 将下一层的节点加入队列
                if (current.left != null) {
                    queue.offer(current.left);
                }
                if (current.right != null) {
                    queue.offer(current.right);
                }
            }
            // 最后一个节点的 next 指向 null
            if (last != null) {
                last.next = null;
            }
        }
        
        return root;
    }
}

117. 填充每个节点的下一个右侧节点指针 II

117. 填充每个节点的下一个右侧节点指针 II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
    public Node connect(Node root) {
          if (root == null) {
            return root;
        }
        
        Queue<Node> queue = new LinkedList<>();
        queue.offer(root);
        
        while (!queue.isEmpty()) {
            int size = queue.size(); 
            Node last = null; 
            
            for (int i = 0; i < size; i++) {
                Node current = queue.poll();
                
                // 连接上一个节点
                if (last != null) {
                    last.next = current;
                }
                
                last = current; 
                // 将下一层的节点加入队列
                if (current.left != null) {
                    queue.offer(current.left);
                }
                if (current.right != null) {
                    queue.offer(current.right);
                }
            }
            // 最后一个节点的 next 指向 null
            if (last != null) {
                last.next = null;
            }
        }
        
        return root;
    }
}

104. 二叉树的最大深度

104. 二叉树的最大深度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int maxDepth(TreeNode root) {
        int deep = 0;
        if(root!=null){
            Queue<TreeNode>queue = new LinkedList<>();
            queue.offer(root);
            while(!queue.isEmpty()){
                int size = queue.size();
                while(size!=0){
                    size--;
                    root = queue.poll();
                    if(root.left!=null){
                        queue.offer(root.left);
                    }
                    if(root.right!=null){
                        queue.offer(root.right);
                    }
                }
                deep++;
            }
        }
        return deep;
    }
}

111. 二叉树的最小深度

111. 二叉树的最小深度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public int minDepth(TreeNode root) {
        int deep = 0;
        if (root != null) {
            Queue<TreeNode> queue = new LinkedList<>();
            queue.offer(root);
            while (!queue.isEmpty()) {
                deep++;
                int size = queue.size();
                while (size != 0) {
                    size--;
                    root = queue.poll();
                    if (root.left != null) {
                        queue.offer(root.left);
                    }
                    if (root.right != null) {
                        queue.offer(root.right);
                    }
                    //叶子节点，左右都为空
                    if(root.left==null&&root.right==null){
                        return deep;
                    }
                }
                
            }
        }
        return deep;
    }
}

二叉树的属性

101. 对称二叉树

101. 对称二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public boolean isSymmetric(TreeNode root) {
        if (root == null) {
            return false;
        }
        return isSymmetry(root.left, root.right);
    }

    public boolean isSymmetry(TreeNode left, TreeNode right) {
        if (left == null && right == null) {
            return true;
        } else if (left != null && right != null) {
            // 两个都存在并且值相等，求左边的左子树和右边的右子树；左边的右子树和右边的左子树是否相等
            return left.val == right.val && isSymmetry(left.left, right.right) && isSymmetry(left.right, right.left);
        }
        // 一个为空，一个不为空
        return false;
    }
}

迭代如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
  /**
     * 迭代法
     * 使用双端队列，相当于两个栈
     */
    public boolean isSymmetric2(TreeNode root) {
        Deque<TreeNode> deque = new LinkedList<>();
        deque.offerFirst(root.left);
        deque.offerLast(root.right);
        while (!deque.isEmpty()) {
            TreeNode leftNode = deque.pollFirst();
            TreeNode rightNode = deque.pollLast();
            if (leftNode == null && rightNode == null) {
                continue;
            }
//            if (leftNode == null && rightNode != null) {
//                return false;
//            }
//            if (leftNode != null && rightNode == null) {
//                return false;
//            }
//            if (leftNode.val != rightNode.val) {
//                return false;
//            }
            // 以上三个判断条件合并
            if (leftNode == null || rightNode == null || leftNode.val != rightNode.val) {
                return false;
            }
            deque.offerFirst(leftNode.left);
            deque.offerFirst(leftNode.right);
            deque.offerLast(rightNode.right);
            deque.offerLast(rightNode.left);
        }
        return true;
    }

    /**
     * 迭代法
     * 使用普通队列
     */
    public boolean isSymmetric3(TreeNode root) {
        Queue<TreeNode> deque = new LinkedList<>();
        deque.offer(root.left);
        deque.offer(root.right);
        while (!deque.isEmpty()) {
            TreeNode leftNode = deque.poll();
            TreeNode rightNode = deque.poll();
            if (leftNode == null && rightNode == null) {
                continue;
            }
//            if (leftNode == null && rightNode != null) {
//                return false;
//            }
//            if (leftNode != null && rightNode == null) {
//                return false;
//            }
//            if (leftNode.val != rightNode.val) {
//                return false;
//            }
            // 以上三个判断条件合并
            if (leftNode == null || rightNode == null || leftNode.val != rightNode.val) {
                return false;
            }
            // 这里顺序与使用Deque不同
            deque.offer(leftNode.left);
            deque.offer(rightNode.right);
            deque.offer(leftNode.right);
            deque.offer(rightNode.left);
        }
        return true;
    }

104. 二叉树的最大深度

104. 二叉树的最大深度

前面有用层次遍历的写法，这里递归秒了

1
2
3
4
5
6
7
8
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
    }
}

111. 二叉树的最小深度

111. 二叉树的最小深度

前面层次遍历有迭代的做法，这里用递归，注意怎么定义最小深度的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int minDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        // 下面就跟求最大深度不同了，这里注意用例2的特殊情况，必须都左右都为空才符合条件，一个为空还不行
        if (root.left == null) {
            return minDepth(root.right) + 1;
        }
        if (root.right == null) {
            return minDepth(root.left) + 1;
        }
        // 都不为空
        return 1 + Math.min(minDepth(root.left), minDepth(root.right));
    }
}

222. 完全二叉树的节点个数

222. 完全二叉树的节点个数

直接当做普通二叉树来做

1
2
3
4
5
6
7
8
class Solution {
    public int countNodes(TreeNode root) {
        if(root==null){
            return 0;
        }
        return 1+countNodes(root.left)+countNodes(root.right);
    }
}

借助完全二叉树的性质

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public int countNodes(TreeNode root) {
        if (root == null) {
            return 0;
        }
        // 计算深度
        TreeNode left = root.left;
        TreeNode right = root.right;
        int l = 0, r = 0;
        // 为什么左边一直往左，右边一直往右呢，因为完全二叉树不是满的最后会全往左边靠，这样总会有一个右边为空，数量左右就不相等了
        while (left != null) {
            left = left.left;
            l++;
        }
        while (right != null) {
            right = right.right;
            r++;
        }
        if (l == r) {
            // 满的用公式计算 2<<n 相当于 2的n次方
            return (2 << l) - 1;
        }
        // 最后总会有满的
        return 1 + countNodes(root.left) + countNodes(root.right);
    }
}

110. 平衡二叉树

110. 平衡二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public boolean isBalanced(TreeNode root) {
        if(root==null){
            return true;
        }
        int l = getTreeDeep(root.left);
        int r = getTreeDeep(root.right);
        return Math.abs(l-r)<=1 && isBalanced(root.left) && isBalanced(root.right);
    }

    public int getTreeDeep(TreeNode node){
        if(node==null){
            return 0;
        }
        //求最大树深才对，而不是求个数，求个数就不用max，求最大树深就需要大值了
        return Math.max(getTreeDeep(node.left),getTreeDeep(node.right))+1;
    }
}

上面会进行很多重复计算，比较浪费时间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public boolean isBalanced(TreeNode root) {
        return getTreeDeep(root) != -1;
    }

    public int getTreeDeep(TreeNode node) {
        if (node == null) {
            return 0;
        }
        // 求深度是用后续遍历的，左右后加上中间的
        int l = getTreeDeep(node.left);
        if (l == -1) {
            return -1;
        }
        int r = getTreeDeep(node.right);
        if (r == -1) {
            return -1;
        }
        // 不是平衡树就直接返回了
        if (Math.abs(l - r) > 1) {
            return -1;
        }
        return 1 + Math.max(l, r);
    }
}

257. 二叉树的所有路径

257. 二叉树的所有路径

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {

    List<String> result = new ArrayList<>();

    public List<String> binaryTreePaths(TreeNode root) {
        if (root != null) {
            resolve(root, new ArrayList<Integer>());
        }

        return result;
    }

    // 回溯
    public void resolve(TreeNode root, List<Integer> list) {
        // 加入自己
        list.add(root.val);

        // 如果是叶子节点，构建路径
        if (root.left == null && root.right == null) {
            StringBuilder builder = new StringBuilder();
            for (Integer i : list) {
                builder.append(i);
                builder.append("->");
            }
            // 去掉最后的 "->"
            builder.delete(builder.length() - 2, builder.length());
            result.add(builder.toString());
        } else {
            // 左右子树递归处理
            if (root.left != null) {
                resolve(root.left, list);
                list.remove(list.size() - 1);
            }
            if (root.right != null) {
                resolve(root.right, list);
                list.remove(list.size() - 1);
            }
        }
    }
}

100. 相同的树

100. 相同的树

1
2
3
4
5
6
7
8
9
10
class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        if (p == null && q == null) {
            return true;
        } else if (p != null && q != null) {
            return p.val == q.val && isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
        }
        return false;
    }
}

404. 左叶子之和

404. 左叶子之和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        if(root==null){
            return 0;
        }
        //左叶子，是叶子才是这样
        if(root.left!=null&&root.left.left==null&&root.left.right==null){
            return root.left.val+sumOfLeftLeaves(root.left)+sumOfLeftLeaves(root.right); 
        }else {
            return sumOfLeftLeaves(root.left)+sumOfLeftLeaves(root.right);
        }
   
    }
}

513. 找树左下角的值

513. 找树左下角的值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    //当前最大层，初始为0，后续比这个大就更新，这样保证第一个才更新
    int deep = -1;
    //保存结果
    int result = 0;

    public int findBottomLeftValue(TreeNode root) {
        //迭代层次遍历也行，递归更快，这里保证了root不为空
        dfs(root,0);
        return result;
    }

    public void dfs(TreeNode root,int cur){
        if(cur>deep){
            result = root.val;
            deep = cur;
        }
        //左右不为空才继续递归
        if(root.left!=null){
            dfs(root.left,cur+1);
        }
        if(root.right!=null){
            dfs(root.right,cur+1);
        }
    }
}

112. 路径总和

112. 路径总和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if (root == null) {
            return false;
        }
        return isResult(root, 0, targetSum);
    }

    public boolean isResult(TreeNode node, int temp, int targetSum) {

        temp += node.val;

        if (node.left == null && node.right == null && temp == targetSum) {
            return true;
        }

        boolean l = false;
        boolean r = false;

        if (node.left != null) {
            l = isResult(node.left, temp, targetSum);
        }

        if (node.right != null) {
            r = isResult(node.right, temp, targetSum);
        }

        return l || r;

    }
}

572. 另一棵树的子树

572. 另一棵树的子树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        if (root == null) {
            return subRoot == null;
        }
        return isSame(root, subRoot) || isSubtree(root.left, subRoot) || isSubtree(root.right, subRoot);
    }

    // 看两棵树是否一样
    public boolean isSame(TreeNode tree1, TreeNode tree2) {
        if (tree1 == null && tree2 == null) {
            return true;
        } else if (tree1 != null && tree2 != null) {
            return tree1.val == tree2.val && isSame(tree1.left, tree2.left) && isSame(tree1.right, tree2.right);
        }
        return false;
    }
}

559. N 叉树的最大深度

559. N 叉树的最大深度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int maxDepth(Node root) {
        if (root == null) {
            return 0;
        } else if (root.children == null || root.children.isEmpty()) {
            return 1;
        }
        int max = 0;
        for (Node n : root.children) {
            max = Math.max(max, maxDepth(n));
        }
        return max + 1;
    }
}

迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    /**
     * 迭代法，使用层序遍历
     */
    public int maxDepth(TreeNode root) {
        if(root == null) {
            return 0;
        }
        Deque<TreeNode> deque = new LinkedList<>();
        deque.offer(root);
        int depth = 0;
        while (!deque.isEmpty()) {
            int size = deque.size();
            depth++;
            for (int i = 0; i < size; i++) {
                TreeNode node = deque.poll();
                if (node.left != null) {
                    deque.offer(node.left);
                }
                if (node.right != null) {
                    deque.offer(node.right);
                }
            }
        }
        return depth;
    }
}

二叉树的修改与改造

226. 翻转二叉树

226. 翻转二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public TreeNode invertTree(TreeNode root) {
        invert(root);
        return root;
    }

    // 递归交换左右子树，为空返回
    public void invert(TreeNode node) {
        if (node == null) {
            return;
        }
        TreeNode temp = node.left;
        node.left = node.right;
        node.right = temp;
        invert(node.left);
        invert(node.right);
    }
}

递归很简单搞定，也可以BFS，这里直接贴别人的代码了，太无聊了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) {return null;}
        ArrayDeque<TreeNode> deque = new ArrayDeque<>();
        deque.offer(root);
        while (!deque.isEmpty()) {
            int size = deque.size();
            while (size-- > 0) {
                TreeNode node = deque.poll();
                swap(node);
                if (node.left != null) deque.offer(node.left);
                if (node.right != null) deque.offer(node.right);
            }
        }
        return root;
    }

    public void swap(TreeNode root) {
        TreeNode temp = root.left;
        root.left = root.right;
        root.right = temp;
    }
}

106. 从中序与后序遍历序列构造二叉树

106. 从中序与后序遍历序列构造二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        if (inorder.length == 0) {
            return null;
        }
        // 创建根节点
        TreeNode head = new TreeNode(postorder[postorder.length - 1]);

        // 找到根节点在中序遍历中的位置
        int k;
        for (k = 0; k < inorder.length; k++) {
            if (inorder[k] == postorder[postorder.length - 1]) {
                break;
            }
        }

        // 分别计算左子树和右子树的长度
        int leftLength = k;
        int rightLength = inorder.length - k - 1;

        // 递归构建左子树和右子树（右子树的位置注意，最后一个为头节点不应该包含）
        head.left = buildTree(Arrays.copyOfRange(inorder, 0, leftLength),
                Arrays.copyOfRange(postorder, 0, leftLength));
        head.right = buildTree(Arrays.copyOfRange(inorder, k + 1, inorder.length),
                Arrays.copyOfRange(postorder, leftLength, postorder.length - 1));
        return head;
    }
}

copy出来很浪费时间和空间，不copy用下面的类似题目的方法

105. 从前序与中序遍历序列构造二叉树

105. 从前序与中序遍历序列构造二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        return build(preorder, inorder, 0, preorder.length - 1, 0, inorder.length);
    }

    public TreeNode build(int[] preorder, int[] inorder, int preStart, int preEnd, int inStart, int inEnd) {
        if (preorder.length == 0 || preStart > preEnd) {
            return null;
        }
        // 当前要组装的树的根节点
        TreeNode root = new TreeNode(preorder[preStart]);
        // 左和右
        // 找到当前树根节点在中序数组中的位置，计算左右子树的数组长度
        int k;
        for (k = inStart; k <= inEnd; k++) {
            if (inorder[k] == preorder[preStart]) {
                break;
            }
        }
        // 知道一棵树的长度就行，剩下的分割开就是另一棵树的
        int lenL = k - inStart;
        root.left = build(preorder, inorder, preStart + 1, preStart + 1 + lenL - 1, inStart, k - 1);
        root.right = build(preorder, inorder, preStart + 1 + lenL, preEnd, k + 1, inEnd);
        return root;
    }
}

654. 最大二叉树

654. 最大二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        return build(nums, 0, nums.length - 1);
    }

    public TreeNode build(int[] nums, int start, int end) {
        // 越界构建不了
        if (start > end) {
            return null;
        }
        int big = start;
        for (int i = start + 1; i <= end; i++) {
            // 不会重复，没有相等情况
            if (nums[i] > nums[big]) {
                big = i;
            }
        }
        // 找到最大的
        TreeNode root = new TreeNode(nums[big]);
        root.left = build(nums, start, big - 1);
        root.right = build(nums, big + 1, end);
        return root;
    }
}

617. 合并二叉树

617. 合并二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if (root1 == null) {
            return root2;
        }
        if (root2 == null) {
            return root1;
        }
        // 都不为空合并并递归左右
        root1.val += root2.val;
        root1.left = mergeTrees(root1.left, root2.left);
        root1.right = mergeTrees(root1.right, root2.right);
        return root1;
    }
}

二叉搜索树的属性

700. 二叉搜索树中的搜索

700. 二叉搜索树中的搜索

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        if(root==null){
            return null;
        }
        if(root.val<val){
            //走右边
            return searchBST(root.right,val);
        }
        if(root.val>val){
            //走左边
            return searchBST(root.left,val);
        }
        //相等
        return root; 
    }
}

98. 验证二叉搜索树

98. 验证二叉搜索树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    // max 变量用来保存中序遍历中最后一次访问到的节点。这是因为在中序遍历（左 -> 根 -> 右）中，遍历到的节点值应该是严格递增的
    TreeNode max;

    public boolean isValidBST(TreeNode root) {
        // 真没想出来，就想到中序遍历卡住了
        if (root == null) {
            return true;
        }
        // 先看左边是不是
        boolean l = isValidBST(root.left);
        // 左边不是可以先返回了
        if (!l) {
            return false;
        }
        // 左边都是了，就可以判断根节点有没有比自己左边大就行
        if (max != null && max.val >= root.val) {
            return false;
        }
        // 把当前节点的值更新为 max，以便接下来判断右子树时用到
        max = root;
        // 右边
        return isValidBST(root.right);
    }
}

530. 二叉搜索树的最小绝对差

530. 二叉搜索树的最小绝对差

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {

    TreeNode last;
    int min = Integer.MAX_VALUE;

    public int getMinimumDifference(TreeNode root) {
        midOrder(root);
        return min;
    }

    //二叉搜索树中序遍历是严格递增的
    public void midOrder(TreeNode root){
        if(root==null){
            return;
        }
        midOrder(root.left);
        if(last!=null){
            min = Math.min(min,root.val-last.val);
        }
        last = root;
        midOrder(root.right);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    public int getMinimumDifference(TreeNode root) {
        // 好久没写中序遍历了，怕忘记，这里写写吧,题目说了树不会为空
        // 结果
        int min = Integer.MAX_VALUE;
        // 保存上次访问的节点
        TreeNode last = null;
        Stack<TreeNode> stack = new Stack<>();
        while (root != null || !stack.isEmpty()) {
            // 一路向左
            if (root != null) {
                stack.push(root);
                root = root.left;
            } else {
                // 抛出处理中间的
                root = stack.pop();
                if (last != null) {
                    min = Math.min(min, root.val - last.val);
                }
                last = root;
                // 处理右边的
                root = root.right;
            }
        }
        return min;
    }
}

501. 二叉搜索树中的众数

501. 二叉搜索树中的众数

如果是普通树就需要用Map了，这里的话是二叉搜索树，可以借助他的特性，还要注意考虑只有一个都特殊情况怎么处理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {

    // 保存出现的次数
    int count = 0;
    // 保存上次访问的节点
    TreeNode last;
    // 保存last出现的次数
    int temp = 0;
    // 保存结果
    List<Integer> result = new ArrayList<>();

    public int[] findMode(TreeNode root) {
        midOrder(root);
        int[] nums = new int[result.size()];
        for (int i = 0; i < nums.length; i++) {
            nums[i] = result.get(i);
        }
        return nums;
    }

    public void midOrder(TreeNode root) {
        if (root == null) {
            return;
        }
        midOrder(root.left);
        // 只有一个都特殊情况要考虑
        if (last == null || root.val > last.val) {
            temp = 1;
        } else {
            temp++;
        }
        if (temp > count) {
            count = temp;
            // 要先清空结果，之前的不作数
            result.clear();
            result.add(root.val);
        } else if (temp == count) {
            // 同样数量的情况出现了
            result.add(root.val);
        }
        last = root;
        midOrder(root.right);
    }
}

538. 把二叉搜索树转换为累加树

538. 把二叉搜索树转换为累加树

右->中->左就是倒序了，用一个保存上次的位置的值即可，初始化为0，每次遍历到的加上上次位置的值即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {

    int last = 0;

    public TreeNode convertBST(TreeNode root) {
        convertBSTTree(root);
        return root;
    }

    public void convertBSTTree(TreeNode root) {
        if (root == null) {
            return;
        }
        convertBSTTree(root.right);
        root.val += last;
        last = root.val;
        convertBSTTree(root.left);
    }
}

1038. 从二叉搜索树到更大和树

1038. 从二叉搜索树到更大和树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {

    int last = 0;

    public TreeNode bstToGst(TreeNode root) {
        bstToGstTree(root);
        return root;
    }

    public void bstToGstTree(TreeNode root) {
        if (root == null) {
            return;
        }
        bstToGstTree(root.right);
        root.val += last;
        last = root.val;
        bstToGstTree(root.left);
    }
}

二叉树公共祖先问题

236. 二叉树的最近公共祖先

236. 二叉树的最近公共祖先

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        // 这题看到想到的是如果能从底部到root去遍历就好判断了，但是二叉树都是从顶部来遍历的，做不到，但是后序递归遍历的过程中就可以回传，从下往上
        if (root == null || root == p || root == q) {
            // 当前这个节点为null或者p或者q直接回传就行，说明找到了或者遍历到头没有找到这个节点
            // 这里第二个情况就是如果一个节点是p或者q可以直接返回了，从上面遍历下来第一个遇到的肯定就是最近公共祖先了，不然就没有结果了，直接返回结果就好
            return root;
        }
        // 后序遍历
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);
        // 最后处理回传的结果
        if (left != null && right != null) {
            return root;
        }
        // 有一个为空就返回不为空那个传上来的结果就行，都为null说明下面都没有，直接往上返回null
        if (left == null) {
            return right;
        } else {
            return left;
        }
    }
}

235. 二叉搜索树的最近公共祖先

235. 二叉搜索树的最近公共祖先

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
//递归
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        // 这棵树是二叉搜索树，那么就要借助他的特性，在二叉搜索树中两个节点的公共祖先一定是小于left的大于right的
        // 那么遍历过程中找到的第一个是不是最近公共祖先呢，模拟一下发现是的
        if (root == null) {
            return null;
        }
        if (root.val < p.val && root.val < q.val) {
            // 往右去搜索，太小了
            TreeNode right = lowestCommonAncestor(root.right, p, q);
            // 不为空说明找到结果了
            if (right != null) {
                return right;
            }
        } else if (root.val > p.val && root.val > q.val) {
            // 往左去搜索，太大了
            TreeNode left = lowestCommonAncestor(root.left, p, q);
            if (left != null) {
                return left;
            }
        } else {
            // 找到第一个在中间的，直接返回
            return root;
        }
        return null;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//迭代
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        while (root != null) {
            // 向右搜索，太小了
            if (root.val < p.val && root.val < q.val) {
                root = root.right;
            }
            // 向左搜索，太大了
            else if (root.val > p.val && root.val > q.val) {
                root = root.left;
            }
            // 找到第一个
            else {
                return root;
            }
        }
        return null;
    }
}

二叉搜索树的修改与构造

701. 二叉搜索树中的插入操作

701. 二叉搜索树中的插入操作

没想出来。。。真裂开

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {

    public TreeNode insertIntoBST(TreeNode root, int val) {
        // 其实这题并没有那么难，不需要考虑太多的问题，其实就只需遇到空的位置就插入进去就行了,总会遇到空的
        if (root == null) {
            return new TreeNode(val);
        }
        if (root.val > val) {
            // 往左边遍历去插
            root.left = insertIntoBST(root.left, val);
        } else {
            // 往右边遍历去插
            root.right = insertIntoBST(root.right, val);
        }
        return root;
    }
}

迭代好理解点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if (root == null) {
            return new TreeNode(val);
        }
        TreeNode last = root;
        TreeNode newHead = root;
        while (root != null) {
            last = root;
            if (root.val > val) {
                root = root.left;
            } else {
                root = root.right;
            }
        }
        // 出来说明找到空位置了
        if (last.val > val) {
            last.left = new TreeNode(val);
        } else {
            last.right = new TreeNode(val);
        }
        return newHead;
    }
}

450. 删除二叉搜索树中的节点

450. 删除二叉搜索树中的节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        //递归写法
        if(root==null){
            //不用删除
            return null;
        }else if(root.val==key){
            //左右都为null，直接删除就行
            if(root.left==null&&root.right==null){
                return null;
            }
            //左不空，右空，删除后上一个要指向left
            else if(root.left!=null&&root.right==null){
                return root.left;
            }
            //右不空，同理
            else if(root.right!=null&&root.left==null){
                return root.right;
            }
            //左右都不为空
            else{
                //这里选择让右子树继位
                TreeNode cur = root.right;
                //并且要将左子树放到这个右子树最小值的左边，那最小值怎么求？一直往左就行
                while(cur.left!=null){
                    cur = cur.left;
                }
                cur.left = root.left;
                return root.right;
            }
        }else{
            //不等于怎么半，根据二叉排序树的性质
            if(root.val<key){
                root.right = deleteNode(root.right,key);
            }else{
                root.left = deleteNode(root.left,key);
            }
            //root怎么不用管，最上面处理root了，else才到这里了，root肯定不用理了
            return root;
        }
    }
}

108. 将有序数组转换为二叉搜索树

108. 将有序数组转换为二叉搜索树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        return build(nums,0,nums.length-1);
    }

    public TreeNode build(int[] nums,int start,int end){
        if(start>end){
            return null;
        }
        //平衡就从中间开始构建就好，并且是有序数组就直接构建就行了，保证左边都小，右边都大就行
        int mid = start +(end-start)/2;
        TreeNode root = new TreeNode(nums[mid]);
        //左树
        root.left = build(nums,start,mid-1);
        root.right = build(nums,mid+1,end);
        return root;
    }
}

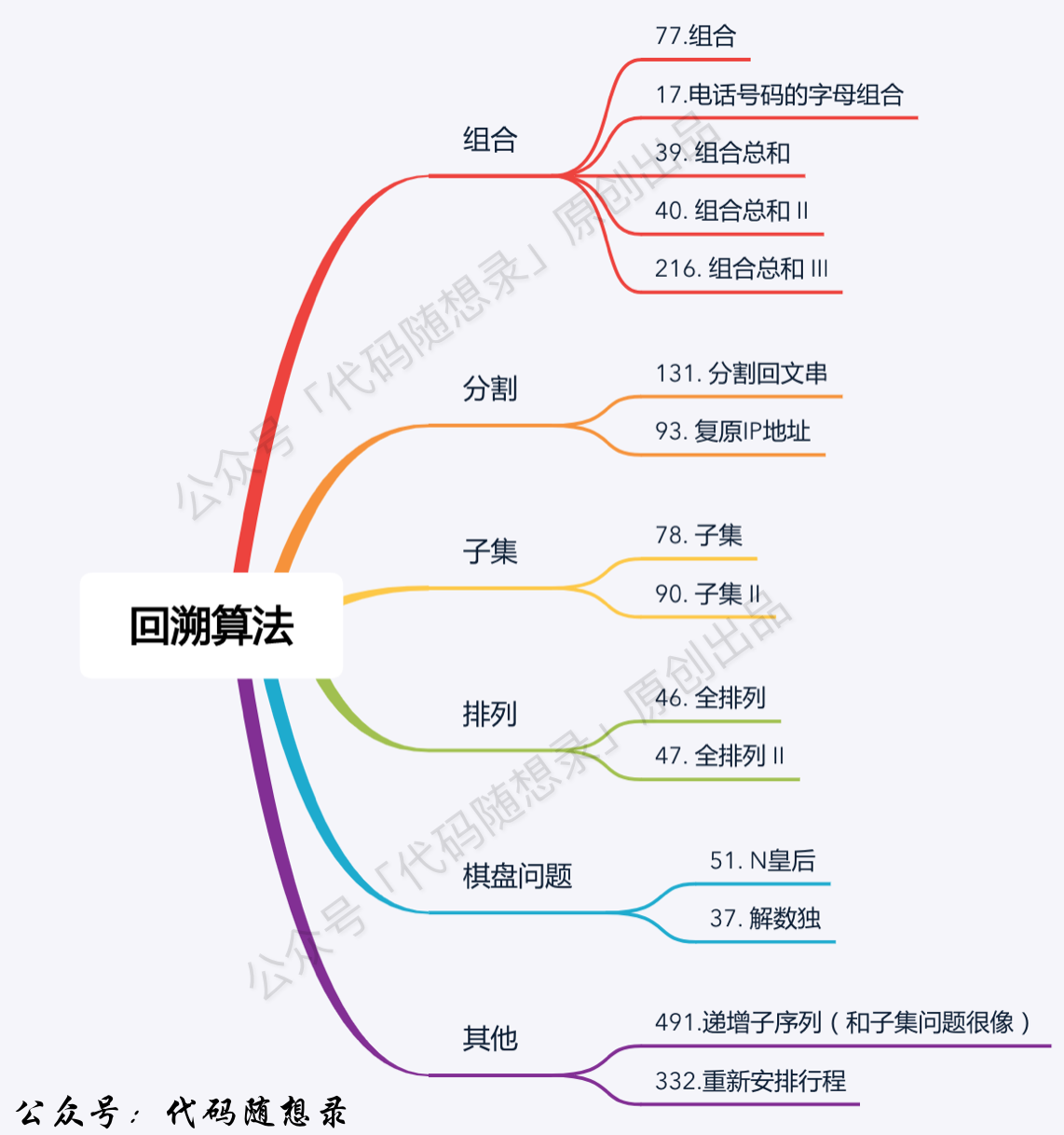
回溯算法

回溯也叫回溯搜索法，是一种搜索的方式，回溯是递归的副产物，有递归就会有回溯，回溯函数就是指一个递归函数。

回溯的本质是穷举，穷举所有可能，然后选出我们想要的答案，如果想让回溯法高效一些，可以加一些剪枝的操作，但也改不了回溯法就是穷举的本质，所以回溯并不是高效的算法，但有些问题只能进行暴力搜索，最多再剪枝一下，没有更高效的算法了。

回溯法解决的问题都可以抽象为树形结构，因为回溯法解决的都是在集合中递归查找子集，集合的大小就构成了树的宽度，递归的深度就构成了树的深度。递归就要有终止条件，所以必然是一棵高度有限的树（N叉树）。

回溯模板

  • 回溯函数模板返回值以及参数
  • 回溯函数终止条件
  • 回溯搜索的遍历过程
1
2
3
4
5
6
7
8
9
10
11
12
void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

能解决的问题

  • 组合问题：N个数里面按一定规则找出k个数的集合
  • 切割问题：一个字符串按一定规则有几种切割方式
  • 子集问题：一个N个数的集合里有多少符合条件的子集
  • 排列问题：N个数按一定规则全排列，有几种排列方式
  • 棋盘问题：N皇后，解数独等等

组合问题

77. 组合

77. 组合

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {

    List<List<Integer>> result = new ArrayList<>();
    List<Integer> temp = new ArrayList<>();

    public List<List<Integer>> combine(int n, int k) {
        backtrack(1, n, k);
        return result;
    }

    // 遍历中每轮要做的就是从开的位置从去遍历到n，本轮加入一个数字，然后去递归
    public void backtrack(int startIndex, int n, int k) {
        if (temp.size() == k) {
            // 加入结果集
            result.add(new ArrayList<>(temp));
            // 中止
            return;
        }
        // 剪枝，也可以在for循环中控制遍历位置，i<=n- (k-temp.size()) +1
        if (temp.size() + n - startIndex + 1 < k) {
            return;
        }

        // 未到中止条件就遍历加入数字
        for (int i = startIndex; i <= n; i++) {
            temp.add(i);
            // 递归
            backtrack(i + 1, n, k);
            // 回溯，删除本轮操作
            temp.remove(temp.size() - 1);
        }
    }
}

39. 组合总和

39. 组合总和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {

    List<List<Integer>> result = new ArrayList<>();
    List<Integer> temp = new ArrayList<>();

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        //排序保证组建往大了加，不会回头，也可以减枝提高效率
        Arrays.sort(candidates);
        backTracking(candidates, target, 0, 0);
        return result;
    }

    public void backTracking(int[] candidates, int target, int index, int sum) {
        if (sum >= target) {
            if (sum == target) {
                result.add(new ArrayList<>(temp));
            }
            return;
        }
        for (int i = index; i < candidates.length; i++) {
            // 减枝
            if (sum + candidates[i] > target) {
                break;
            }
            sum += candidates[i];
            temp.add(candidates[i]);
            // 可重复选，但是排序过了，只会往后相等或大于,index变为i，下次从当前位置开始或者往后，容易错
            backTracking(candidates, target, i, sum);
            // 回溯
            sum -= candidates[i];
            temp.remove(temp.size() - 1);
        }
    }
}

40. 组合总和 II

40. 组合总和 II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {

    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        Arrays.sort(candidates);
        List<List<Integer>> result = new ArrayList<>();
        backTracking(candidates, target, 0, 0, result, new ArrayList<>());
        return result;
    }

    public void backTracking(int[] candidates, int target, int sum, int index, List<List<Integer>> result,
            List<Integer> temp) {
        if (sum == target) {
            result.add(new ArrayList<>(temp));
        }
        for (int i = index; i < candidates.length; i++) {
            // 剪枝
            if (sum + candidates[i] > target) {
                break;
            }
            // 里面有重复元素，需要跳过一样的
            if (i > index && candidates[i] == candidates[i - 1]) {
                continue;
            }
            sum += candidates[i];
            temp.add(candidates[i]);
            // 递归，不能重复，i+1
            backTracking(candidates, target, sum, i + 1, result, temp);
            // 回溯
            sum -= candidates[i];
            temp.remove(temp.size() - 1);
        }
    }
}

216. 组合总和 III

216. 组合总和 III

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {

    List<List<Integer>> result = new ArrayList<>();
    List<Integer> temp = new ArrayList<>();
    int sum = 0;

    // 不能重复的组合就都往后走就行
    public List<List<Integer>> combinationSum3(int k, int n) {
        backTracking(k, n, 1);
        return result;
    }

    public void backTracking(int k, int n, int startIndex) {
        if (temp.size() >= k || sum >= n) {
            if (temp.size() == k && sum == n) {
                // 加入结果集
                result.add(new ArrayList<>(temp));
            }
            return;
        }

        // 往后遍历即可,剪枝
        for (int i = startIndex; i <= 9 - (k - temp.size()) + 1; i++) {
            sum += i;
            temp.add(i);
            // 递归
            backTracking(k, n, i + 1);
            // 回溯
            temp.remove(temp.size() - 1);
            sum -= i;
        }
    }
}

17. 电话号码的字母组合

17. 电话号码的字母组合

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {

    List<String>result = new ArrayList<>();
    char[] temp;
    Map<Character,String>map = new HashMap<>();

    public List<String> letterCombinations(String digits) {
        temp = new char[digits.length()];
        //保存映射到Map
        map.put('2',"abc");
        map.put('3',"def");
        map.put('4',"ghi");
        map.put('5',"jkl");
        map.put('6',"mno");
        map.put('7',"pqrs");
        map.put('8',"tuv");
        map.put('9',"wxyz");
        if(digits.length()!=0){
            backTracking(digits,0);
        }
        return result;
    }

    public void backTracking(String digits,int index){
        if(index==digits.length()){
            result.add(new String(temp));
            return;
        }
        char c = digits.charAt(index);
        String s = map.get(c);
        for(int i = 0;i<s.length();i++){
            temp[index] = s.charAt(i);
            backTracking(digits,index+1);
            temp[index] = ' ';
        }
    }
}

排列问题

46. 全排列

46. 全排列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public List<List<Integer>> permute(int[] nums) {
        boolean[] isVisited = new boolean[nums.length];
        List<List<Integer>> result = new ArrayList<>();
        List<Integer> temp = new ArrayList<>();
        backTracking(result, new ArrayList<>(), isVisited, nums);
        return result;
    }

    // 可能会回头从头再来，那么就需要保存是否使用过
    public void backTracking(List<List<Integer>> result,
            List<Integer> temp, boolean[] isVisited, int[] nums) {
        if (temp.size() == nums.length) {
            // 保存
            result.add(new ArrayList<>(temp));
        }
        for (int i = 0; i < nums.length; i++) {
            if (isVisited[i]) {
                continue;
            }
            temp.add(nums[i]);
            isVisited[i] = true;
            // 递归
            backTracking(result, temp, isVisited, nums);
            // 回溯
            temp.remove(temp.size() - 1);
            isVisited[i] = false;
        }
    }
}

47. 全排列 II

47. 全排列 II

去重那里没想出来，还是要画图来看的好

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
    public List<List<Integer>> permuteUnique(int[] nums) {
        // 还要强调的是去重一定要对元素进行排序，这样我们才方便通过相邻的节点来判断是否重复使用了。
        Arrays.sort(nums);
        List<List<Integer>> result = new ArrayList<>();
        backTracking(result, new ArrayList<>(), new boolean[nums.length], nums);
        return result;
    }

    public void backTracking(List<List<Integer>> result,
            List<Integer> temp, boolean[] isVisited, int[] nums) {
        if (temp.size() == nums.length) {
            // 加入结果
            result.add(new ArrayList<>(temp));
            return;
        }
        for (int i = 0; i < nums.length; i++) {
            // 如果同一树层nums[i - 1]使用过则直接跳过
            if (i != 0 && nums[i] == nums[i - 1] && !isVisited[i - 1]) {
                continue;
            }
            if (isVisited[i]) {
                continue;
            }
            isVisited[i] = true;
            temp.add(nums[i]);
            // 递归
            backTracking(result, temp, isVisited, nums);
            // 回溯
            isVisited[i] = false;
            temp.remove(temp.size() - 1);
        }
    }
}

子集问题

78. 子集

78. 子集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>>result = new ArrayList<>();
        backTracking(result,new ArrayList<>(),nums,0);
        return result;
    }

    public void backTracking(List<List<Integer>>result,
    List<Integer>temp,int[] nums,int index){
            if(index>=nums.length){
                //加入结果
                result.add(new ArrayList<>(temp));
                return;
            }
            for(int i = index;i<=nums.length;i++){
                //因为要空进行中断，所以要考虑越界，并且最开始大于就加入
                if(i==nums.length){
                    backTracking(result,temp,nums,i+1);
                    continue;
                }
                //不用去重，排序后往后就不会出现重复的了
                temp.add(nums[i]);
                backTracking(result,temp,nums,i+1);
                temp.remove(temp.size()-1);
            }

    }
}

也可以不靠终止条件，而是记录每个结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    List<List<Integer>> result = new ArrayList<>();// 存放符合条件结果的集合
    LinkedList<Integer> path = new LinkedList<>();// 用来存放符合条件结果
    public List<List<Integer>> subsets(int[] nums) {
        subsetsHelper(nums, 0);
        return result;
    }

    private void subsetsHelper(int[] nums, int startIndex){
        result.add(new ArrayList<>(path));//「遍历这个树的时候，把所有节点都记录下来，就是要求的子集集合」。
        if (startIndex >= nums.length){ //终止条件可不加
            return;
        }
        for (int i = startIndex; i < nums.length; i++){
            path.add(nums[i]);
            subsetsHelper(nums, i + 1);
            path.removeLast();
        }
    }
}

90. 子集 II

90. 子集 II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        // 需要去重，排序才好去重
        Arrays.sort(nums);
        List<List<Integer>> result = new ArrayList<>();
        backTracking(result, new ArrayList<>(), nums, 0);
        return result;
    }

    public void backTracking(List<List<Integer>> result,
            List<Integer> temp, int[] nums, int index) {
        // 这里用跟前面的不同思路，其实整个树没排除掉的加入就好
        result.add(new ArrayList<>(temp));
        // 不需要结束了其实
        for (int i = index; i < nums.length; i++) {
            // 去重,注意是跳过，不是break，不然1 1 2 2就被异常终止了
            if (i != index && nums[i] == nums[i - 1]) {
                continue;
            }
            temp.add(nums[i]);
            // 递归
            backTracking(result, temp, nums, i + 1);
            // 回溯
            temp.remove(temp.size() - 1);
        }
    }
}

分割问题

131. 分割回文串

131. 分割回文串

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution {
    public List<List<String>> partition(String s) {
        // 暴力列举所有组合
        List<List<String>> result = new ArrayList<>();
        backTracking(result, new ArrayList<>(), s, 0);
        return result;
    }

    public void backTracking(List<List<String>> result,
            List<String> temp, String s, int index) {
        if (index == s.length()) {
            // 加入结果
            result.add(new ArrayList<>(temp));
        }
        for (int i = index; i < s.length(); i++) {
            String wait = s.substring(index, i + 1);
            // 剪枝
            if (isMoslems(wait)) {
                temp.add(wait);
                // 递归
                backTracking(result, temp, s, i + 1);
                // 回溯
                temp.remove(temp.size() - 1);
            }
        }
    }

    // 判断某个字符串是不是回文
    public boolean isMoslems(String s) {
        if (s == null || s.length() == 0) {
            return false;
        }
        int left = 0, right = s.length() - 1;
        while (left < right) {
            if (s.charAt(left) != s.charAt(right)) {
                return false;
            }
            left++;
            right--;
        }
        return true;
    }
}

93. 复原 IP 地址

93. 复原 IP 地址

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
class Solution {
    public List<String> restoreIpAddresses(String s) {
        // 暴力求解所有可能性
        List<String> result = new ArrayList<>();
        backTracking(result, new StringBuilder(), s, 1, 0);
        return result;
    }

    public void backTracking(List<String> result, StringBuilder builder, String s, int deep, int index) {
        if (deep > 4) {
            // 全分完才算
            if (index >= s.length()) {
                // 加入结果
                result.add(builder.toString());
            }
            return;
        }
        // 避免剩下不能划分了，减枝
        for (int i = index; i < s.length() - (4 - deep); i++) {
            String temp = s.substring(index, i + 1);
            // 剪枝
            if (isCurrent(temp)) {
                builder.append(temp);
                if (deep != 4) {
                    builder.append(".");
                }
                // 递归
                backTracking(result, builder, s, deep + 1, i + 1);
                // 回溯
                int length = builder.length();
                if (deep == 4) {
                    builder.delete(length - temp.length(), length);
                } else {
                    builder.delete(length - temp.length() - 1, length);
                }
            }
        }
    }

    // 看某个字符串是否符合要求
    public boolean isCurrent(String s) {
        if (s.isBlank()) {
            return false;
        }
        if (s.length() > 1 && s.charAt(0) == '0') {
            return false;
        }
        try {
            int num = Integer.parseInt(s);
            return num >= 0 && num <= 255;
        } catch (Exception e) {
            return false;
        }
    }
}

棋盘问题

都是困难级别的题目

51. N 皇后

51. N 皇后

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
class Solution {
    public List<List<String>> solveNQueens(int n) {
        List<List<String>> result = new ArrayList<>();
        char[][] board = new char[n][n];
        for (int i = 0; i < n; i++) {
            Arrays.fill(board[i], '.');
        }
        backTracking(n, 0, board, result);
        return result;
    }

    // 检查在这个位置放皇后是否合法
    public boolean isLegal(int row, int column, int n, char[][] board) {
        // 检查这个列上是否有放过皇后了，相当于剪枝了，由于是每一层遍历下来的，每个横向只会放一个，不会有问题
        for (int i = 0; i < row; i++) {
            if (board[i][column] == 'Q') {
                return false;
            }
        }

        // 检查从这个位置向左上角跑到边界是否有放过皇后
        for (int i = row - 1, j = column - 1; i >= 0 && j >= 0; i--, j--) {
            if (board[i][j] == 'Q') {
                return false;
            }
        }

        // 检查从这个位置向右上角跑到边界看是否放过皇后
        for (int i = row - 1, j = column + 1; i >= 0 && j < n; i--, j++) {
            if (board[i][j] == 'Q') {
                return false;
            }
        }

        return true;
    }

    // 回溯
    public void backTracking(int n, int deep, char[][] board, List<List<String>> result) {
        if (deep == n) {
            List<String> temp = new ArrayList<>();
            for (int i = 0; i < n; i++) {
                temp.add(new String(board[i]));
            }
            result.add(temp);
            return;
        }
        // 每一层都从第一个位置看能不能填，能填就填去递归，不能就回溯
        for (int j = 0; j < n; j++) {
            // 可以填
            if (isLegal(deep, j, n, board)) {
                board[deep][j] = 'Q';
                // 递归
                backTracking(n, deep + 1, board, result);
                // 回溯
                board[deep][j] = '.';
            }
        }
    }

}

37. 解数独

37. 解数独

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
class Solution {
    public void solveSudoku(char[][] board) {
        solveSudokuHelper(board);
    }

    // 检查当前位置填写这个数字是否合法,这题固定了就是9*9的
    public boolean isLegal(int row, int column, char num, char[][] board) {
        // 检查行是否出现过这个数字
        for (int j = 0; j < 9; j++) {
            if (board[row][j] == num) {
                return false;
            }
        }

        // 检查列是否出现过这个数字
        for (int i = 0; i < 9; i++) {
            if (board[i][column] == num) {
                return false;
            }
        }

        // 检查宫格是否出现过这个数字,找到当前这个位置对应宫格的左上角的下标开始遍历
        int top = row / 3 * 3, start = column / 3 * 3;
        for (int i = top; i < top + 3; i++) {
            for (int j = start; j < start + 3; j++) {
                if (board[i][j] == num) {
                    return false;
                }
            }
        }

        return true;
    }

    // 递归
    public boolean solveSudokuHelper(char[][] board) {
        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                if (board[i][j] == '.') {
                    // 当前位置没填过，尝试0-9
                    for (int num = 1; num <= 9; num++) {
                        // 巧妙转换int为char
                        char c = (char) (num + '0');
                        if (isLegal(i, j, c, board)) {
                            board[i][j] = c;
                            // 递归
                            if (solveSudokuHelper(board)) {
                                // 找到一组合适可以终止了
                                return true;
                            }
                            // 回溯
                            board[i][j] = '.';
                        }
                    }
                    // 这里可以返回了，每个遍历只处理一个位置,每个数字都不合适
                    return false;
                }
            }
        }
        // 遍历完没有返回false，说明找到了合适棋盘位置了
        return true;
    }
}

这里一定需要能判断是否处理完，不然不知道什么时候跳出，等自然循环跳出最后都恢复为原状了，也可以如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
class Solution {
    public void solveSudoku(char[][] board) {
        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                if (board[i][j] == '.') {
                    // 当前位置没填过，尝试0-9
                    for (int num = 1; num <= 9; num++) {
                        // 巧妙转换int为char
                        char c = (char) (num + '0');
                        if (isLegal(i, j, c, board)) {
                            board[i][j] = c;
                            // 递归
                            solveSudoku(board);
                            // 如果递归填满后，不需要回溯，可以直接返回
                            if (isSolved(board)) return;
                            // 回溯
                            board[i][j] = '.';
                        }
                    }
                    return;
                }
            }
        }
    }

    // 检查当前位置填写这个数字是否合法,这题固定了就是9*9的
    public boolean isLegal(int row, int column, char num, char[][] board) {
        // 检查行是否出现过这个数字
        for (int j = 0; j < 9; j++) {
            if (board[row][j] == num) {
                return false;
            }
        }

        // 检查列是否出现过这个数字
        for (int i = 0; i < 9; i++) {
            if (board[i][column] == num) {
                return false;
            }
        }

        // 检查宫格是否出现过这个数字,找到当前这个位置对应宫格的左上角的下标开始遍历
        int top = row / 3 * 3, start = column / 3 * 3;
        for (int i = top; i < top + 3; i++) {
            for (int j = start; j < start + 3; j++) {
                if (board[i][j] == num) {
                    return false;
                }
            }
        }

        return true;
    }

       // 检查数独是否已经被完全解开
    public boolean isSolved(char[][] board) {
        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                if (board[i][j] == '.') {
                    return false;
                }
            }
        }
        return true;
    }
}

其他问题

491. 非递减子序列

491. 非递减子序列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {

    List<List<Integer>>result = new ArrayList<>();
    List<Integer>temp = new ArrayList<>();

    public List<List<Integer>> findSubsequences(int[] nums) {
        //这里不能排序了，因为要按照原本顺序来
        backTracking(nums,0);
        return result;
    }

    public void backTracking(int[]nums,int index){
        if(temp.size()>=2){
            result.add(new ArrayList<>(temp));
        }

        Set<Integer>used = new HashSet<>();

        for(int i = index;i<nums.length;i++){
            //去重，这里没有排序，不能单纯跟前一个比较来进行去重，这里用Set快速去重，同一层用过的就不能再使用了
            if(used.contains(nums[i])){
                continue;
            }
            //减枝
            if(temp.size()>0&&temp.get(temp.size()-1)>nums[i]){
                continue;
            }
            temp.add(nums[i]);
            used.add(nums[i]);
            //递归
            backTracking(nums,i+1);
            //回溯
            temp.remove(temp.size()-1);
        }
    }
}

332. 重新安排行程

332. 重新安排行程

1
void

贪心算法

贪心的本质是选择每一阶段的局部最优，从而达到全局最优。

刷题或者面试的时候，手动模拟一下感觉可以局部最优推出整体最优，而且想不到反例，那么就试一试贪心。

并没有太多的技巧性，贪心想不到反例就可能可以用，不行就只能动规了，但很多时候还是需要数学理论来支持的，有些没写过类似的不会就是不会了

贪心算法一般分为如下四步：

  • 将问题分解为若干个子问题
  • 找出适合的贪心策略
  • 求解每一个子问题的最优解
  • 将局部最优解堆叠成全局最优解

但其实很多时候用不上，想得到贪心策略很重要，想不出啥步骤都没用

简单难度

455. 分发饼干

455. 分发饼干

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int findContentChildren(int[] g, int[] s) {
        // 先排序，从小到大满足最接近的人，能满足就满足，不能只能换大饼干，因为排序了，这个饼干小的不能满足，大胃口的更不能满足
        Arrays.sort(g);
        Arrays.sort(s);
        int count = 0;
        int i = 0, j = 0;
        while (i < g.length && j < s.length) {
            if (s[j] >= g[i]) {
                i++;
                j++;
                count++;
            } else {
                j++;
            }
        }
        return count;
    }
}

1005. K 次取反后最大化的数组和

1005. K 次取反后最大化的数组和

下面是自己写的，时间复杂度和空间复杂度都比较高

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int largestSumAfterKNegations(int[] nums, int k) {
        PriorityQueue<Integer> queue = new PriorityQueue<>();
        for (int i : nums) {
            queue.offer(i);
        }
        while (k != 0) {
            queue.offer(-queue.poll());
            k--;
        }
        int sum = 0;
        while (!queue.isEmpty()) {
            sum += queue.poll();
        }
        return sum;
    }
}

版本2也是不断排序，没啥好看的了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
class Solution {
    public int largestSumAfterKNegations(int[] nums, int K) {
    	// 将数组按照绝对值大小从大到小排序，注意要按照绝对值的大小
	nums = IntStream.of(nums)
		     .boxed()
		     .sorted((o1, o2) -> Math.abs(o2) - Math.abs(o1))
		     .mapToInt(Integer::intValue).toArray();
	int len = nums.length;	    
	for (int i = 0; i < len; i++) {
	    //从前向后遍历，遇到负数将其变为正数，同时K--
	    if (nums[i] < 0 && K > 0) {
	    	nums[i] = -nums[i];
	    	K--;
	    }
	}
	// 如果K还大于0，那么反复转变数值最小的元素，将K用完

	if (K % 2 == 1) nums[len - 1] = -nums[len - 1];
	return Arrays.stream(nums).sum();

    }
}

// 版本二：排序数组并贪心地尽可能将负数翻转为正数，再根据剩余的k值调整最小元素的符号，从而最大化数组的总和。
class Solution {
    public int largestSumAfterKNegations(int[] nums, int k) {
        if (nums.length == 1) return nums[0];

        // 排序：先把负数处理了
        Arrays.sort(nums); 

        for (int i = 0; i < nums.length && k > 0; i++) { // 贪心点, 通过负转正, 消耗尽可能多的k
            if (nums[i] < 0) {
                nums[i] = -nums[i];
                k--;
            }
        }

        // 退出循环, k > 0 || k < 0 (k消耗完了不用讨论)
        if (k % 2 == 1) { // k > 0 && k is odd：对于负数：负-正-负-正
            Arrays.sort(nums); // 再次排序得到剩余的负数，或者最小的正数
            nums[0] = -nums[0];
        }
        // k > 0 && k is even，flip数字不会产生影响: 对于负数: 负-正-负；对于正数：正-负-正 

        int sum = 0;
        for (int num : nums) { // 计算最大和
            sum += num;
        }
        return sum;
    }
}

860. 柠檬水找零

860. 柠檬水找零

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public boolean lemonadeChange(int[] bills) {
        int fiveCount = 0, tenCount = 0;
        for (int i = 0; i < bills.length; i++) {
            if (bills[i] == 5) {
                fiveCount++;
            } else if (bills[i] == 10) {
                // 找一张5
                fiveCount--;
                tenCount++;
                if (fiveCount < 0) {
                    return false;
                }
            } else {
                // 可以找一张10或5，也可以3张5
                if (tenCount > 0) {
                    fiveCount--;
                    tenCount--;
                } else {
                    fiveCount -= 3;
                }
                if (fiveCount < 0 || tenCount < 0) {
                    return false;
                }
            }

        }
        return true;
    }
}

中等难度

序列问题

376. 摆动序列

376. 摆动序列

思考有偏差，裂开，没有考虑到一路向下和一路向上的更新情况

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int wiggleMaxLength(int[] nums) {
        // 这里的子序列是可以通过删除元素来形成的，这里nums一定不为空
        int result = 1, pre = 0;
        // 这里不用last保存上一个元素，跟前一个做比较就好，因为一直向下的话还是要更新的其实，但前面写的错的没有更新
        for (int i = 1; i < nums.length; i++) {
            int current = nums[i] - nums[i - 1];
            if ((current < 0 && pre >= 0) || (current > 0 && pre <= 0)) {
                result++;
                pre = current;
            }
        }
        return result;
    }
}

738. 单调递增的数字

738. 单调递增的数字

没想到贪心啊，暴力超时的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int monotoneIncreasingDigits(int n) {
        char[] chars = String.valueOf(n).toCharArray();
        int start = chars.length;
        for (int i = chars.length - 2; i >= 0; i--) {
            // 从后往前，如果一个位置大于下个位置
            if (chars[i] > chars[i + 1]) {
                chars[i]--;
                start = i + 1;
            }
        }
        for (int i = start; i < chars.length; i++) {
            chars[i] = '9';
        }
        return Integer.valueOf(new String(chars));
    }
}

股票问题

121. 买卖股票的最佳时机

121. 买卖股票的最佳时机

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int maxProfit(int[] prices) {
        int max = 0;
        int min = prices[0];
        for (int i = 1; i < prices.length; i++) {
            if (prices[i] > min) {
                int temp = prices[i] - min;
                max = Math.max(max, temp);
            } else {
                min = prices[i];
            }
        }
        return max;
    }
}

动态规划，顺便放这里了，后面动规部分可以直接跳转来这里看，我是觉得这里用动规是有点难理解的，回头多看几遍吧

代码随想录 (programmercarl.com)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int maxProfit(int[] prices) {
        // 这里用动规做法做一下
        int length = prices.length;
        if (length <= 1) {
            return 0;
        }
        // dp每一行表示当前遍历到的天数下，纵坐标的0为持有股票的最大收益，1为不持有股票都最大收益，持有股票不一定是今天买入的，也可能是昨天买入的
        int[][] dp = new int[length][2];
        // 初始化，初始化的值可以根据下面的递推方程看初始化为什么合适，初始谁合适，这里就需要初始化第0行，第 0
        // 天持有股票，那么我们唯一的选择是买入股票，这时收益是负的，即 -prices[0]
        dp[0][0] = -prices[0];
        dp[0][1] = 0;
        for (int i = 1; i < length; i++) {
            // dp[i][0]为什么不是dp[i - 1][1] - prices[i]去做比较，这是因为这题是要求全程只能买卖一次
            dp[i][0] = Math.max(dp[i - 1][0], -prices[i]);
            // 看是卖出合适还是维持之前的合适
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
        }
        return dp[length - 1][1];
    }
}

122. 买卖股票的最佳时机 II

122. 买卖股票的最佳时机 II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int maxProfit(int[] prices) {
        // 不断找上升区间
        int result = 0, min = prices[0];
        for (int i = 1; i < prices.length; i++) {
            if (prices[i] < prices[i - 1]) {
                // 下降的上一个就是最大的上升区间
                result += (prices[i - 1] - min);
                min = prices[i];
            }
        }
        // 避免一路递增,最后是赚的就卖出
        if (prices[prices.length - 1] - min > 0) {
            result += (prices[prices.length - 1] - min);
        }
        return result;
    }
}

假如第 0 天买入，第 3 天卖出，那么利润为：prices[3] - prices[0]。

相当于(prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0])。

更简化

1
2
3
4
5
6
7
8
9
10
// 贪心思路
class Solution {
    public int maxProfit(int[] prices) {
        int result = 0;
        for (int i = 1; i < prices.length; i++) {
            result += Math.max(prices[i] - prices[i - 1], 0);
        }
        return result;
    }
}

动态规划解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int maxProfit(int[] prices) {
        // 动规做一下
        int length = prices.length;
        if (length <= 1) {
            return 0;
        }
        // dp跟上一题表示一样，0表示持有的最大收益，1表示不持有的最大收益
        int[][] dp = new int[length][2];
        // 初始化
        dp[0][0] = -prices[0];
        dp[0][1] = 0;
        // 后一天的结果很前一天的情况有关，正序遍历
        for (int i = 1; i < length; i++) {
            // 看是继续持有收益多还是之前不持有买入当天的收益多
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
            // 看是之前不持有收益多，还是卖出收益多
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
        }
        return dp[length - 1][1];
    }
}

714. 买卖股票的最佳时机含手续费

714. 买卖股票的最佳时机含手续费

这里的贪心是真的睿智，贪心思想可以浓缩成一句话，即当我们卖出一支股票时，我们就立即获得了以相同价格并且免除手续费买入一支股票的权利。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int maxProfit(int[] prices, int fee) {
        // 最大收益
        int max = 0;
        // 当前手上的股票的买入价格,巧妙把手续费加在买入的时候
        int buy = prices[0] + fee;
        for (int i = 1; i < prices.length; i++) {
            // 当前股票买入价格更低，不如在这时候买入
            if (prices[i] + fee < buy) {
                buy = prices[i] + fee;
            }
            // 如果当前股票价格大于buy，那么直接买入股票获得prices[i]-fee的收入，但是这可能不是全局最优解，那么就需要一个反悔机制，这里再更新buy为prices[i]，如果下面继续递增，那么就会prices[i+1]-prices[i]，加上之前的收益prices[i]-buy，就是收入
            else if (prices[i] > buy) {
                max += prices[i] - buy;
                buy = prices[i];
            }
        }
        // 对于其余的情况，prices[i] 落在区间 [buy−fee,buy]
        // 内，它的价格没有低到我们放弃手上的股票去选择它，也没有高到我们可以通过卖出获得收益，因此我们不进行任何操作
        return max;
    }
}

动规

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int maxProfit(int[] prices, int fee) {
        int length = prices.length;
        if (length <= 1) {
            return 0;
        }
        int[] dp = new int[2];
        // 初始化
        dp[0] = -prices[0];
        // 递归
        for (int i = 1; i < length; i++) {
            dp[0] = Math.max(dp[0], dp[1] - prices[i]);
            dp[1] = Math.max(dp[1], dp[0] + prices[i] - fee);
        }
        return dp[1];
    }
}

两个维度权衡问题

遇到两个维度的时候，一定要想如何确定一个维度，然后再按照另一个维度重新排序，如果两个维度一起考虑肯定会顾此失彼

406. 根据身高重建队列

406. 根据身高重建队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int[][] reconstructQueue(int[][] people) {
        // 之前考虑的都是按h从小排到大发现很难想出来，其实是从大排到小先，这样就可以很快知道前面有几个比你大的，直接在考虑k维度的时候插入到下标位置就说明前面比你大的有几个，局部最优并且也是整体最优解
        Arrays.sort(people, (a, b) -> {
            // 两个身高相等就看谁k小在前面
            if (a[0] == b[0])
                return a[1] - b[1];
            return b[0] - a[0];
        });

        // 考虑k维度
        List<int[]> temp = new ArrayList<>();
        for (int[] ints : people) {
            temp.add(ints[1], ints);
        }
        int[][] reuslt = new int[people.length][2];
        for (int i = 0; i < temp.size(); i++) {
            reuslt[i] = temp.get(i);
        }
        return reuslt;
    }
}

135. 分发糖果

135. 分发糖果

力扣上定义是困难，这里考虑局部的时候如果左右都兼顾那么就会顾此失彼，这里使用两次贪心的

  • 一次是从左到右遍历，只比较右边孩子评分比左边大的情况。
  • 一次是从右到左遍历，只比较左边孩子评分比右边大的情况。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int candy(int[] ratings) {
        // 第一次先从左往右去发，左边比右边大才发+1，不然就是1
        int[] candy = new int[ratings.length];
        candy[0] = 1;
        for (int i = 1; i < ratings.length; i++) {
            candy[i] = ratings[i] > ratings[i - 1] ? candy[i - 1] + 1 : 1;
        }
        // 第二次就从后往左去看那个比后一个大，此时 左边的糖果应该 取本身的糖果数（符合比它左边大） 和 右边糖果数 + 1 二者的最大值，这样才符合
        // 它比它左边的大，也比它右边大
        for (int i = ratings.length - 2; i >= 0; i--) {
            if (ratings[i] > ratings[i + 1]) {
                // 当前比后面的大，需要满足大的结果
                candy[i] = Math.max(candy[i], candy[i + 1] + 1);
            }
        }
        // 这样两次贪心是最优解，可以统计结果
        int result = 0;
        for (int i : candy) {
            result += i;
        }
        return result;
    }
}

困难难度

区间问题

55. 跳跃游戏

55. 跳跃游戏

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public boolean canJump(int[] nums) {
        if (nums.length == 1) {
            return true;
        }
        // 让当前可跳的步数最多
        int balance = nums[0], i = 0;
        while (balance != 0 && i != nums.length) {
            // 移动一步，消耗balance
            balance--;
            if (nums[i] > balance) {
                balance = nums[i];
            }
            i++;
        }
        return i == nums.length ? true : false;
    }
}

45. 跳跃游戏 II

45. 跳跃游戏 II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public int jump(int[] nums) {
        if (nums == null || nums.length == 0 || nums.length == 1) {
            return 0;
        }
        int result = 0;
        // 最远可以跳到的位置
        int maxCanJump = 0;
        // 当前跳跃的边界
        int end = 0;
        for (int i = 0; i < nums.length; i++) {
            // 更新最远可以跳到的位置
            maxCanJump = Math.max(maxCanJump, i + nums[i]);
            // 跳到的边界就必须要跳跃一次了,遍历完了里面所有的情况，maxCanJump为里面某个位置可以跳到的最远的位置，自然跳到那个位置啊，那end就更新为那个位置的边界
            if (i == end) {
                // 跳一步，跳到范围内最远到达的位置，具体哪个位置不用管
                result++;
                // 更新边界
                end = maxCanJump;
            }
            // 看是否能跳到尾部，能就提前结束
            if (end >= nums.length - 1) {
                break;
            }
        }
        return result;
    }
}

452. 用最少数量的箭引爆气球

452. 用最少数量的箭引爆气球

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public int findMinArrowShots(int[][] points) {
        int result = 0;
        //直接减可能比较会内存溢出，这里要Integer.compare
        Arrays.sort(points, (a, b) -> Integer.compare(a[0], b[0]));
        int[] range = new int[2];
        range[0] = points[0][0];
        range[1] = points[0][1];
        for (int i = 1; i < points.length; i++) {
            if (points[i][0] > range[1]) {
                // 超出范围了，后面的都是另外区间的了，在range内发射一箭就好
                result++;
                // 更新范围
                range[0] = points[i][0];
                range[1] = points[i][1];
            } else {
                // 在旧区间操作,缩小范围，左右都要判断，或者最开始按照结束的距离大小从小到大排序就好，其实发现这里关注的是结束位置
                range[0] = Math.max(points[i][0], range[0]);
                range[1] = Math.min(points[i][1], range[1]);
            }
        }
        // 最后一个区间发射一支
        return result + 1;
    }
}

这样更简洁

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import java.util.Arrays;

class Solution {
    public int findMinArrowShots(int[][] points) {
        if (points == null || points.length == 0) return 0;

        // 按区间结束位置排序
        Arrays.sort(points, (a, b) -> Integer.compare(a[1], b[1]));

        int result = 1;  // 至少需要一箭
        int end = points[0][1];  // 第一个气球的结束位置

        for (int i = 1; i < points.length; i++) {
            // 如果当前气球的起点大于上一个气球的结束位置，则需要发射一箭
            if (points[i][0] > end) {
                result++;
                end = points[i][1];  // 更新结束位置为当前气球的结束位置
            }
        }

        return result;
    }
}

435. 无重叠区间

435. 无重叠区间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int eraseOverlapIntervals(int[][] intervals) {
        Arrays.sort(intervals,(a,b)->Integer.compare(a[0],b[0]));

        int count = 0;
        int end = intervals[0][1];
        for(int i = 1;i<intervals.length;i++){
            if(end>intervals[i][0]){
                //有重叠要移除一个，具体移除
                count++;
                //移除掉结尾更晚的那个，创造更多机会
                end = Math.min(end,intervals[i][1]);
            }else{
                //无重叠
                end = intervals[i][1];
            }
        }
        return count;
    }
}

763. 划分字母区间

763. 划分字母区间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public List<Integer> partitionLabels(String s) {
        // 确实想不出来，这里先统计每个字母出现的最后的下标
        int[] hash = new int[26];

        List<Integer> result = new ArrayList<>();

        for (int i = 0; i < s.length(); i++) {
            hash[s.charAt(i) - 'a'] = i;
        }

        // 保存上次加入的最后的下标
        int last = -1;
        // 当前区间里的最后下标
        int index = 0;

        // 如果i == 当前字母最后出现的下标就可以分割了
        for (int i = 0; i < s.length(); i++) {

            index = Math.max(index, hash[s.charAt(i) - 'a']);
            if (i == index) {
                // 加入集合
                result.add(i - last);
                last = i;
            }
        }

        return result;
    }
}

56. 合并区间

56. 合并区间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
    public int[][] merge(int[][] intervals) {
        Arrays.sort(intervals, (a, b) -> Integer.compare(a[0], b[0]));
        List<int[]> temp = new ArrayList<>();

        int start = intervals[0][0];
        int end = intervals[0][1];

        for (int i = 0; i < intervals.length; i++) {
            if (end >= intervals[i][0]) {
                // 有重叠就合并为一个区间
                end = Math.max(end, intervals[i][1]);
            } else {
                // 无重叠保存上次的区间，新开一个区间了
                int[] ints = new int[2];
                ints[0] = start;
                ints[1] = end;
                temp.add(ints);
                // 开新区间
                start = intervals[i][0];
                end = intervals[i][1];
            }
        }
        // 保存最后一个区间
        int[] ints = new int[2];
        ints[0] = start;
        ints[1] = end;
        temp.add(ints);

        int[][] result = new int[temp.size()][2];
        for (int i = 0; i < temp.size(); i++) {
            result[i] = temp.get(i);
        }
        return result;
    }
}

其他

53. 最大子数组和

53. 最大子数组和

贪心

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public int maxSubArray(int[] nums) {
        // 加上自己如果都没自己大，那自己就是当前最大的开始
        int result = nums[0], temp = nums[0];
        for (int i = 1; i < nums.length; i++) {
            temp = Math.max(temp + nums[i], nums[i]);
            result = temp > result ? temp : result;
        }
        return result;
    }
}

动规

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int maxSubArray(int[] nums) {
            //带点贪心思想，要么加上前面的大要么从自己新开始大
            int[] dp = new int[nums.length];
            int result = nums[0];
            dp[0] = nums[0];
            for(int i =1;i<nums.length;i++){
                //递推公式
                dp[i] = Math.max(dp[i-1]+nums[i],nums[i]);
                result = dp[i]>result?dp[i]:result;
            }
            return result;
    }
}

134. 加油站

134. 加油站

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        // 总加油量
        int totalGas = 0;
        // 总消耗量
        int totalCostGas = 0;
        // 开始区间的开始第一个的坐标
        int index = 0;
        // 区间内的油箱余量，为0就说明不可能到达这个站，就不应该从上次的开始区间的第一个坐标开始
        int range = 0;
        for (int i = 0; i < gas.length; i++) {
            totalGas += gas[i];
            totalCostGas += cost[i];

            range = range + gas[i] - cost[i];

            if (range < 0) {
                // 从下个位置开始为开始区间，跟最大子序和有点像
                index = i + 1;
                range = 0;
            }
        }
        return totalGas >= totalCostGas ? index : -1;
    }
}

968. 监控二叉树

968. 监控二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {

    int result = 0;

    public int minCameraCover(TreeNode root) {
        if (putCamera(root) == 0) {
            // 对根节点的状态做检验,防止根节点是无覆盖状态
            result++;
        }
        return result;
    }

    // 状态0：无覆盖 状态1：有摄像头 状态2：有覆盖
    public int putCamera(TreeNode root) {
        // 终止条件
        if (root == null) {
            // 为空遍历到了叶子节点，叶子节点必须是有覆盖的
            return 2;
        }
        // 后序遍历
        int left = putCamera(root.left);
        int right = putCamera(root.right);

        // 左右都有覆盖，这里就是无覆盖的，2是无摄像头但被覆盖了
        if (left == 2 && right == 2) {
            return 0;
        }
        // 左右有一个未被覆盖，需要放置一个，能覆盖到下面
        else if (left == 0 || right == 0) {
            result++;
            return 1;
        }
        // 左右至少存在一个摄像头，能覆盖到
        else {
            return 2;
        }

    }
}

动态规划

动态规划，英文：Dynamic Programming，简称DP，如果某一问题有很多重叠子问题，使用动态规划是最有效的。

所以动态规划中每一个状态一定是由上一个状态推导出来的，这一点就区分于贪心，贪心没有状态推导，而是从局部直接选最优的。

对于动态规划问题，我将拆解为如下五步曲，这五步都搞清楚了，才能说把动态规划真的掌握了！

  1. 确定dp数组（dp table）以及下标的含义
  2. 确定递推公式
  3. dp数组如何初始化
  4. 确定遍历顺序
  5. 举例推导dp数组

找问题的最好方式就是把dp数组打印出来，看看究竟是不是按照自己思路推导的！

做动规的题目，写代码之前一定要把状态转移在dp数组的上具体情况模拟一遍，心中有数，确定最后推出的是想要的结果。

基础题目

509. 斐波那契数

509. 斐波那契数

1
2
3
4
5
6
7
8
9
class Solution {
    public int fib(int n) {
        // 递推公式题目给出了，f(0) = 0,f(1) = 1,之后f(n) = f(n-1) + f(n-2)
        if (n == 0 || n == 1) {
            return n;
        }
        return fib(n - 1) + fib(n - 2);
    }
}

递归好理解，但这里迭代快很多

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int fib(int n) {
        // 递推公式题目给出了，f(0) = 0,f(1) = 1,之后f(n) = f(n-1) + f(n-2)
        if (n == 0 || n == 1) {
            return n;
        }
        int first = 0, second = 1;
        for (int i = 2; i <= n; i++) {
            int temp = first + second;
            first = second;
            second = temp;
        }
        return second;
    }
}

非压缩版本

1
2
3
4
5
6
7
8
9
10
11
12
13
//非压缩状态的版本
class Solution {
    public int fib(int n) {
        if (n <= 1) return n;             
        int[] dp = new int[n + 1];
        dp[0] = 0;
        dp[1] = 1;
        for (int index = 2; index <= n; index++){
            dp[index] = dp[index - 1] + dp[index - 2];
        }
        return dp[n];
    }
}

70. 爬楼梯

70. 爬楼梯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int climbStairs(int n) {
        //这个跟斐波那契递推一样，差一步或者两步直接走就行，那么就是F(n-1)+F(n-2)，1只有一种，2有2种，3有3种，4有5种
        if(n<=2){
            return n; 
        }
        int first = 1,second = 2;
        for(int i = 3;i<=n;i++){
            int temp = first+second;
            first = second;
            second = temp;
        }
        return second;
    }
}

746. 使用最小花费爬楼梯

746. 使用最小花费爬楼梯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int minCostClimbingStairs(int[] cost) {
        // 前面斐波那契数列刚好是可以简化的，这里用不简化的，就需要按照常规的动态规划，需要一个数组来保存之前的状态
        int[] dp = new int[cost.length + 1];
        // 可以从0或者1开始，这里需要一个初始值，可以从0和1开始，那么0和1初始化为0即可
        dp[0] = 0;
        dp[1] = 0;
        for (int i = 2; i <= cost.length; i++) {
            // 动态规划方程
            dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
        }
        return dp[dp.length - 1];
    }
}

62. 不同路径

62. 不同路径

还有究极节省内存就是用一行保存dp即可，因为其实每次只用到一行

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int uniquePaths(int m, int n) {
        //只能向下或向右一步，那么最左边和最上边一行都只有一种可能性
        int[][] dp = new int[m][n];
        for(int i = 0;i<m;i++){
            for(int j = 0;j<n;j++){
                //只有一种可能性
                if(i==0||j==0){
                    dp[i][j] = 1;
                    continue;
                }
                //动态规划方程,从左边来或者从上边来
                dp[i][j] = dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
}

63. 不同路径 II

63. 不同路径 II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int[][] dp = new int[obstacleGrid.length][obstacleGrid[0].length];
        // 第一个位置,如果有障碍后面会变回来
        dp[0][0] = 1;
        for (int i = 0; i < obstacleGrid.length; i++) {
            for (int j = 0; j < obstacleGrid[0].length; j++) {
                // 动态规划方程
                // 有障碍不能到达，那这个位置就是0可能性
                if (obstacleGrid[i][j] == 1) {
                    dp[i][j] = 0;
                    continue;
                }
                // 无障碍，这里要考虑只有一行或者一列，其中一个为阻碍的情况，那么阻碍后面都为0
                if (i - 1 >= 0 && j - 1 >= 0) {
                    dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
                } else if (i - 1 >= 0) {
                    dp[i][j] = dp[i - 1][j];
                } else if (j - 1 >= 0) {
                    dp[i][j] = dp[i][j - 1];
                }

            }
        }
        return dp[obstacleGrid.length - 1][obstacleGrid[0].length - 1];
    }
}

343. 整数拆分

343. 整数拆分

这个要借助数学知识，真看不出来，拆分后数值近似相等最后相乘是最大的

动态规划，本题关键在于理解递推公式！| LeetCode：343. 整数拆分_哔哩哔哩_bilibili

首先定义dp[i]，dp[i]是指i拆分后得到的最大的乘积，i拆分为两个数的时候一个拆分为j另一个就是i-j，那三个数的时候就是j和dp[i-j]，只能说恍然大悟，看视频讲的很好

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int integerBreak(int n) {
        int[] dp = new int[n + 1];
        // 初始
        dp[2] = 1;
        for (int i = 3; i <= n; i++) {
            // 拆分,这里j小于i也可以，但是可以优化为下面这个，因为拆分两个数就是要尽可能让两个数相等
            for (int j = 1; j <= i / 2; j++) {
                // 这里还要跟dp[i]比是因为前面dp[i]会在拆分过程中出现过变化了，需要比较一下
                dp[i] = Math.max(dp[i], Math.max(j * (i - j), j * dp[i - j]));
            }
        }
        return dp[n];
    }
}

这个也可以用贪心，这个需要数学证明合理性

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int integerBreak(int n) {
        if (n == 2) return 1;
        if (n == 3) return 2;
        if (n == 4) return 4;
        int result = 1;
        while (n > 4) {
            result *= 3;
            n -= 3;
        }
        result *= n;
        return result;
    }
};

96. 不同的二叉搜索树

96. 不同的二叉搜索树

直接拿代码随想录官网的图过来了，大致思路下面也有，图更直观

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int numTrees(int n) {
        // 这道题目需要去画一下看一下具体怎么生成的，1 1；2
        // 2从3开始，1为顶23为右，23对应2的情况就是2种，2为顶1为左2为右，左右对应1的情况就是1*1；同理看下去
        int[] dp = new int[n + 1];
        if (n <= 2) {
            return n;
        }
        dp[0] = 1;
        dp[1] = 1;
        dp[2] = 2;
        for (int k = 3; k <= n; k++) {
            // 转移方程
            for (int i = 0, j = k - 1; i <= k - 1 && j >= 0; i++, j--) {
                dp[k] += dp[i] * dp[j];
            }
        }
        return dp[n];
    }
}

背包问题

01背包

46. 携带研究材料（第六期模拟笔试）

46. 携带研究材料（第六期模拟笔试） (kamacoder.com)

力扣没有01背包，这题跟01背包原题很像

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
import java.util.Scanner;

public class Main{
    public static void main (String[] args) {
        Scanner scanner = new Scanner(System.in);
        //m为材料数量
        int m = scanner.nextInt();
        //n为行李容量
        int n = scanner.nextInt();
        int[] weight = new int[m];
        int[] values = new int[m];
        for(int i = 0;i<m;i++){
            weight[i] = scanner.nextInt();
        }
        for(int i = 0;i<m;i++){
            values[i] = scanner.nextInt();
        }
        
        //dp[i][j]表示第i件物品和空间容量为j时最大价值
        int[][] dp = new int[m][n+1];
        
        //初始化，第一行重量够了装第一个进去
        for(int i = weight[0];i<=n;i++){
            dp[0][i] = values[0];
        }
        
        for(int i = 1;i<m;i++){
            for(int j = 0;j<=n;j++){
                //不够装就不能装
                if(j<weight[i]){
                    dp[i][j] = dp[i-1][j];
                }else{
                    //看装的价值大还是不装价值大
                    dp[i][j] = Math.max(
                        dp[i-1][j],dp[i-1][j-weight[i]]+values[i]);
                }
            }
        }
        System.out.println(dp[m-1][n]);
    }
}

416. 分割等和子集

416. 分割等和子集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
    public boolean canPartition(int[] nums) {
        // 这题用回溯暴力所有可能性会超时
        // 选和不选某个元素并且只能选择一次就是01背包
        int sum = 0;
        for (int i : nums) {
            sum += i;
        }
        // 奇数肯定做不到
        if (sum % 2 != 0) {
            return false;
        }
        // 背包容量就是一半，下面开始01背包
        sum /= 2;
        int[][] dp = new int[nums.length][sum + 1];
        // 初始值
        for (int i = nums[0]; i <= sum; i++) {
            dp[0][i] = nums[0];
        }
        // 可以滚动数组来优化
        for (int i = 1; i < nums.length; i++) {
            for (int j = 1; j <= sum; j++) {
                // 看够不够装
                if (nums[i] > j) {
                    // 不够
                    dp[i][j] = dp[i - 1][j];
                } else {
                    // 够装，看装还是不装,dp[i-1][j]是不装，dp[i-1][j-nums[i]]就是装，求最大能装去逼近sum
                    dp[i][j] = Math.max(dp[i - 1][j], nums[i] + dp[i - 1][j - nums[i]]);
                }
            }
        }
        return dp[nums.length - 1][sum] == sum ? true : false;
    }
}

1049. 最后一块石头的重量 II

1049. 最后一块石头的重量 II

本题其实就是尽量让石头分成重量相同的两堆，相撞之后剩下的石头最小，这样就化解成01背包问题了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public int lastStoneWeightII(int[] stones) {
        // 划分为两堆，两堆尽可能靠近
        int sum = 0;
        for (int i : stones) {
            sum += i;
        }
        int temp = sum;
        sum /= 2;
        // dp[i][j]的i为当前选择第几块石头，j为当前剩余容量，dp就是在当前情况能能选择的最大重量，可以滚动数组优化
        int[][] dp = new int[stones.length][sum + 1];
        // 初始化
        for (int i = stones[0]; i <= sum; i++) {
            dp[0][i] = stones[0];
        }
        // 开始填充dp数组
        for (int i = 1; i < stones.length; i++) {
            for (int j = 0; j <= sum; j++) {
                // 看够不够装
                if (stones[i] > j) {
                    dp[i][j] = dp[i - 1][j];
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - stones[i]] + stones[i]);
                }
            }
        }
        // 返回大撞小的值
        return (temp - dp[stones.length - 1][sum]) - dp[stones.length - 1][sum];
    }
}

494. 目标和

494. 目标和

这题暴力回溯会超时，先贴出解答，后面有解析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public int findTargetSumWays(int[] nums, int target) {
        int sum = 0;
        for (int i : nums) {
            sum += i;
        }
        // 排除掉明确得不出结果的情况
        if ((sum + target) % 2 != 0) {
            return 0;
        }
        // 下面这个就是说明target太大或者太小了，找不到组合
        if (Math.abs(target) > sum) {
            return 0;
        }
        // 这里用循环dp练练手
        int bagSize = (sum + target) / 2;
        int[] dp = new int[bagSize + 1];
        // 初始化,0容量不放就是1种情况呗
        dp[0] = 1;
        for (int i = 0; i < nums.length; i++) {
            // 按照二维来说，nums[i]比j大的就维持上层的结果就好，就不用更新，那j就要从nums[i]到bgSize，这里逆着遍历是因为如果从小到大小的被更新就拿不到上层的值了
            for (int j = bagSize; j >= nums[i]; j--) {
                // 这里二维下是上层的可能组合数量+选择当前数字后组合数量，这里上层的就是dp[j]没更新的时候，那+=就好
                dp[j] += dp[j - nums[i]];
            }
        }
        return dp[bagSize];
    }
}

假设加法的总和为x，那么减法对应的总和就是sum - x。

所以我们要求的是 x - (sum - x) = target

x = (target + sum) / 2

此时问题就转化为，用nums装满容量为x的背包，有几种方法。

这里的x，就是bagSize，也就是我们后面要求的背包容量。

大家看到(target + sum) / 2 应该担心计算的过程中向下取整有没有影响。

这么担心就对了，例如sum是5，target是2 的话其实就是无解的，所以：

1
2
（C++代码中，输入的S 就是题目描述的 target）
if ((target + sum) % 2 == 1) return 0; // 此时没有方案

同时如果target 的绝对值已经大于sum，那么也是没有方案的。

1
if (abs(target) > sum) return 0; // 此时没有方案

之后拿题目例子来看，可以知道dp[i] [j]如下，但是这里dp表示的是有多少可能性，第一行需要初始化，第一列同样需要初始化

474. 一和零

474. 一和零

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        // 经典01背包是只需要考虑装的物品和重量两个维度，这里需要考虑三个维度，但可以跟二维一样，借助循环数组思想优化到二维，但只是优化dp，遍历还是要遍历三层

        int[][] dp = new int[m + 1][n + 1];

        // 遍历物品
        for (String str : strs) {

            // 统计一下当前遍历到的str的1的个数和0的个数
            int oneCount = 0, zeroCount = 0;
            for (char c : str.toCharArray()) {
                if (c == '1') {
                    oneCount++;
                } else {
                    zeroCount++;
                }
            }

            // 只更新能放的部分,并且这里二维的都需要借助上层的结果，都需要倒序遍历
            for (int i = m; i >= zeroCount; i--) {
                for (int j = n; j >= oneCount; j--) {
                    // 当前需要加一个子集
                    dp[i][j] = Math.max(dp[i][j], dp[i - zeroCount][j - oneCount] + 1);
                }
            }

        }

        return dp[m][n];

    }
}

01背包基础上对滚动数组理解

其实就是把dp的二维数组压缩到一维数组

1
2
3
4
5
6
for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

    }
}

这里大家发现和二维dp的写法中，遍历背包的顺序是不一样的！

二维dp遍历的时候，背包容量是从小到大，而一维dp遍历的时候，背包是从大到小。

为什么呢？

倒序遍历是为了保证物品i只被放入一次！。但如果一旦正序遍历了，那么物品0就会被重复加入多次！

举一个例子：物品0的重量weight[0] = 1，价值value[0] = 15

如果正序遍历

dp[1] = dp[1 - weight[0]] + value[0] = 15

dp[2] = dp[2 - weight[0]] + value[0] = 30

此时dp[2]就已经是30了，意味着物品0，被放入了两次，所以不能正序遍历。

为什么倒序遍历，就可以保证物品只放入一次呢？

倒序就是先算dp[2]

dp[2] = dp[2 - weight[0]] + value[0] = 15 （dp数组已经都初始化为0）

dp[1] = dp[1 - weight[0]] + value[0] = 15

所以从后往前循环，每次取得状态不会和之前取得状态重合，这样每种物品就只取一次了。

那么问题又来了，为什么二维dp数组遍历的时候不用倒序呢？

因为对于二维dp，dp[i][j]都是通过上一层即dp[i - 1][j]计算而来，本层的dp[i][j]并不会被覆盖！

再来看看两个嵌套for循环的顺序，代码中是先遍历物品嵌套遍历背包容量，那可不可以先遍历背包容量嵌套遍历物品呢？

不可以！

因为一维dp的写法，背包容量一定是要倒序遍历（原因上面已经讲了），如果遍历背包容量放在上一层，那么每个dp[j]就只会放入一个物品，即：背包里只放入了一个物品。

所以一维dp数组的背包在遍历顺序上和二维其实是有很大差异的！，这一点大家一定要注意。****

完全背包

322. 零钱兑换

322. 零钱兑换

第一次的思路，时间复杂度太高

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public int coinChange(int[] coins, int amount) {
        
        //dp保存遍历到当前硬币的情况下最少需要的硬币个数
        int[] dp = new int[amount+1];
        //初始化，0肯定是0，初始化比amount大即可
        Arrays.fill(dp,amount+1);
        dp[0] = 0;

        for(int i = 0;i<coins.length;i++){
            //倒序并且最多到硬币大小的容量才能装了
            for(int j = amount;j>=coins[i];j--){

                //看当前容量下最多能装多少个当前遍历到的零钱，要遍历所有个数去查询上层，看最小可能性是哪个
                for(int k = 1;k<=j/coins[i];k++){

                    dp[j] = Math.min(dp[j],dp[j-k*coins[i]]+k);

                }
            }
        }

        return dp[amount]>amount ?-1:dp[amount];

    }
}

改进

遍历 amount 的目的：我们希望找到每个 i 金额所需的最少硬币数，外层循环从小到大依次处理每个可能的金额（从 1 到 amount）。这样，当前金额 i 是基于之前的计算结果（dp[i - coin]）更新的。

遍历 coins 的目的：对于每一个金额 i，我们要尝试所有不同面值的硬币，看看哪个硬币能让我们使用的硬币数量最少。因此，内层循环遍历每一个硬币，找到当前金额的最优解。

状态转移方程：

1
dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int coinChange(int[] coins, int amount) {
        
        //dp保存遍历到当前硬币的情况下最少需要的硬币个数
        int[] dp = new int[amount+1];
        //初始化，0肯定是0，初始化比amount大即可
        Arrays.fill(dp,amount+1);
        dp[0] = 0;

        for(int i = 0;i<coins.length;i++){
            //完全背包，正序遍历，受上次更新结果的影响
            for(int j = coins[i];j<=amount;j++){
                //这样遍历当然也可以,先遍历amount再遍历coins也可以
                dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);
            }
        }

        return dp[amount]>amount ?-1:dp[amount];

    }
}

518. 零钱兑换 II

518. 零钱兑换 II

忘记了为什么是这个遍历顺序就去看看思路吧

代码随想录 (programmercarl.com)

如果求组合数就是外层for循环遍历物品，内层for遍历背包（无顺序）。

如果求排列数就是外层for遍历背包，内层for循环遍历物品（有顺序）。

像上面的求最小数量的什么顺序都可以

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int change(int amount, int[] coins) {
        int[] dp = new int[amount+1];
        //初始化dp数组，表示金额为0时只有一种情况，也就是什么都不装
        dp[0] = 1;

        for(int coin:coins){
            //这里正序,coin是可以多次选择的，01背包只能选择一次需要保证这次更新不会影响下次更新，而完全背包是需要受上次更新的影响的
            for(int j = coin;j<=amount;j++){
                dp[j]+=dp[j-coin];
            }
        }

        return dp[amount];
    }
}

377. 组合总和 Ⅳ

377. 组合总和 Ⅳ

这里需要考虑顺序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int combinationSum4(int[] nums, int target) {
        int[] dp = new int[target + 1];
        dp[0] = 1;
        // 这里需要考虑顺序，那么就先遍历target
        for (int i = 0; i <= target; i++) {
            // 数量不确定，正序遍历，前面的结果会影响后面的结果
            for (int j = 0; j < nums.length; j++) {
                if (i >= nums[j]) {
                    // 递推公式一般是这个
                    dp[i] += dp[i - nums[j]];
                }
            }
        }
        return dp[target];
    }
}

JZ71 跳台阶扩展问题

跳台阶扩展问题_牛客题霸_牛客网 (nowcoder.com)

这里之前找规律类斐波那契也可以解决，这里用完全背包再解决一次罢了，跟上面代码一模一样，这里放一下斐波那契的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import java.util.*;


public class Solution {
    public int jumpFloorII (int number) {
        //跟普通的跳台阶很像，但是就是不是只能1步和2步了，而是前面的可能的总和+1，因为自己永远能一步迈上去，这里result保存当前这层的结果，lastSum保存之前所有层数的可能的总和
        int lastSum = 0, result = 0;
        for (int i = 0; i < number; i++) {
            result = lastSum + 1;
            lastSum += result;
        }
        return result;
    }
}

279. 完全平方数

279. 完全平方数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int numSquares(int n) {
        // 完全平方数一看其实就是1^2,2^2,3^2,4^2
        int[] dp = new int[n + 1];
        Arrays.fill(dp, n + 1);
        dp[0] = 0;
        // 这里求最小值，遍历的先后顺序就不需要考虑了
        for (int i = 1; i <= (int) Math.sqrt(n); i++) {
            for (int j = i * i; j <= n; j++) {
                // 这里j是背包容量
                dp[j] = Math.min(dp[j], dp[j - i * i] + 1);
            }
        }

        return dp[n];
    }
}

139. 单词拆分

139. 单词拆分

举一反三想出来了，一次ac，双爽

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        int length = s.length();
        boolean[] dp = new boolean[length + 1];
        dp[0] = true;
        // 这里可以使用多次，完全背包，全排列，先遍历背包
        for (int i = 0; i <= length; i++) {
            for (int j = 0; j < wordDict.size(); j++) {
                // 够装
                int wordLength = wordDict.get(j).length();
                if (wordLength <= i) {
                    // 当前从结尾来看跟当前单词是否相等并且前半段之前是否能找到相等的情况，最后就是还要和dp[i]求或，因为可能之前能找到了，找到了就一定有可能了，不能改变他
                    dp[i] = (dp[i - wordLength] && s.substring(i - wordLength, i).equals(wordDict.get(j))) || dp[i];
                }
            }
        }
        return dp[length];
    }
}

打家劫舍

198. 打家劫舍

198. 打家劫舍

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int rob(int[] nums) {
        int[] dp = new int[nums.length + 1];
        // 为了方便下面的转移方程的表示，这里加多一个，那么dp多一个在开头
        dp[1] = nums[0];
        for (int i = 2; i <= nums.length; i++) {
            // 转移方程，要么偷旁边的，要么偷间隔的，看哪种情况多偷哪个
            dp[i] = Math.max(dp[i - 2] + nums[i - 1], dp[i - 1]);
        }
        return dp[nums.length];
    }
}

213. 打家劫舍 II

213. 打家劫舍 II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public int rob(int[] nums) {
        //相较于打家劫舍第一个区别这里是循环，那就是偷不偷第一个，偷第一个就不能偷最后一个，不偷第一个就能偷最后一个
        //只有一个,直接返回
        if(nums.length==1){
            return nums[0];
        }
        // 为了方便下面的转移方程的表示，这里加多一个，那么dp多一个在开头
        int[] dp = new int[nums.length + 1];

        //偷第一个
        dp[1] = nums[0];
        for (int i = 2; i < nums.length; i++) {
            // 转移方程，要么偷旁边的，要么偷间隔的，看哪种情况多偷哪个
            dp[i] = Math.max(dp[i - 2] + nums[i - 1], dp[i - 1]);
        }
        int temp = dp[nums.length-1];

        //不偷第一个
        dp = new int[nums.length+1];
        for (int i = 2; i <= nums.length; i++) {
            // 转移方程，要么偷旁边的，要么偷间隔的，看哪种情况多偷哪个
            dp[i] = Math.max(dp[i - 2] + nums[i - 1], dp[i - 1]);
        }
        temp = Math.max(temp,dp[nums.length]);

        return temp;
    }
}

337. 打家劫舍 III

337. 打家劫舍 III

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
    public int rob(TreeNode root) {
        postOrder(root);
        return root.val;
    }

    public void postOrder(TreeNode root) {
        // 只有一个入口，最后从入口拿值是最好的，最后要是入口，就得后序遍历
        if (root == null) {
            return;
        }
        postOrder(root.left);
        postOrder(root.right);
        // 后续遍历
        int l1 = 0, l2 = 0, r1 = 0, r2 = 0;
        int l = 0, r = 0;
        if (root.left != null) {
            l = root.left.val;
            if (root.left.left != null) {
                l1 = root.left.left.val;
            }
            if (root.left.right != null) {
                l2 = root.left.right.val;
            }
        }
        if (root.right != null) {
            r = root.right.val;
            if (root.right.left != null) {
                r1 = root.right.left.val;
            }
            if (root.right.right != null) {
                r2 = root.right.right.val;
            }
        }
        // 偷下一层不能偷自己，偷下下层能偷自己，下层和下下层是后续遍历都处理过了，保存了dp最优解，偷是最优解
        root.val = Math.max(l + r, root.val + r1 + r2 + l1 + l2);
    }
}

股票问题

123. 买卖股票的最佳时机 III

123. 买卖股票的最佳时机 III

不能同时参与多笔交易（必须在再次购买前出售掉之前的股票），理解初始化很重要

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public int maxProfit(int[] prices) {
        // 这里直接放内存优化版本了，具体内容去看解析吧
        int length = prices.length;
        if (length <= 1) {
            return 0;
        }
        // 存储两次交易的状态就行了
        int[] dp = new int[4];
        // 初始化，这个很重要
        // dp[0]代表第一次交易的买入
        dp[0] = -prices[0];
        // dp[1]代表第一次交易的卖出
        dp[1] = 0;
        // dp[2]代表第二次交易的买入,其实相当于第0天第一次买入了，第一次卖出了，然后再买入一次（就是第二次买入）
        dp[2] = -prices[0];
        // dp[3]代表第二次交易的卖出
        dp[3] = 0;
        // 递推
        for (int i = 1; i < length; i++) {
            dp[0] = Math.max(dp[0], 0 - prices[i]);
            dp[1] = Math.max(dp[1], dp[0] + prices[i]);
            // 第二次要加上第一次不持有的
            dp[2] = Math.max(dp[2], dp[1] - prices[i]);
            dp[3] = Math.max(dp[3], dp[2] + prices[i]);
        }
        return dp[3];
    }
}

188. 买卖股票的最佳时机 IV

188. 买卖股票的最佳时机 IV

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public int maxProfit(int k, int[] prices) {
        // 那就根据前面的最多买卖2次的思路来写就行了,为了下面遍历方便，在最开始加一个，初始为0即可，不操作状态
        int[] dp = new int[2 * k + 1];
        dp[0] = 0;
        // 初始值很重要
        for (int j = 1; j <= k; j++) {
            dp[j * 2 - 1] = -prices[0];
            dp[j * 2] = 0;
        }
        // 递推
        for (int i = 1; i < prices.length; i++) {
            // 填写这一行
            for (int j = 1; j <= k; j++) {
                // 基于上次的持有和不持有的情况，本轮持有就看上轮继续持有还是不持有买入，本轮不持有就看继续上轮不持有还是持有卖出
                dp[j * 2 - 1] = Math.max(dp[j * 2 - 1], dp[j * 2 - 2] - prices[i]);
                dp[j * 2] = Math.max(dp[j * 2], dp[j * 2 - 1] + prices[i]);
            }
        }
        return dp[2 * k];

    }
}

309. 买卖股票的最佳时机含冷冻期

309. 买卖股票的最佳时机含冷冻期

结合前面几题理解不同状态的设置，突然恍然大悟

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public int maxProfit(int[] prices) {
        int length = prices.length;
        if (length <= 1) {
            return 0;
        }
        // 有些题解是三个状态的，容易把自己绕进去
        // 0状态为持有（今天买入or维持之前的买入状态）
        // 1状态为今天卖出状态，之前为持有状态
        // 2状态为维持卖出状态，前天可能为冻结期，可能之前就是冻结期了
        // 3状态为冻结状态，前天一定为1状态（并且这个状态只有一天）
        int[][] dp = new int[length][4];
        // 初始化,持有股票
        dp[0][0] = -prices[0];
        // 递推
        for (int i = 1; i < length; i++) {
            // 之前状态可能为持有，可能为冻结，可能为持续卖出
            dp[i][0] = Math.max(dp[i - 1][0], Math.max(dp[i - 1][2] - prices[i], dp[i - 1][3] - prices[i]));
            // 之前状态为持有
            dp[i][1] = dp[i - 1][0] + prices[i];
            // 之前的状态为持续卖出或者冻结，如果前状态为卖出，也就是1那么这里应该是3，只有2才可能这里为2
            dp[i][2] = Math.max(dp[i - 1][2], dp[i - 1][3]);
            // 之前状态为卖出状态
            dp[i][3] = dp[i - 1][1];
        }
        // 返回值，看1 2 3哪种状态收入多，0状态还未卖出，收益不完整，比较了没意义
        return Math.max(dp[length - 1][1], Math.max(dp[length - 1][2], dp[length - 1][3]));
    }
}

先写出上面未优化版本，优化就简单了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    public int maxProfit(int[] prices) {
        int length = prices.length;
        if (length <= 1) {
            return 0;
        }
        // 有些题解是三个状态的，容易把自己绕进去
        // 0状态为持有（今天买入or维持之前的买入状态）
        // 1状态为今天卖出状态，之前为持有状态
        // 2状态为维持卖出状态，前天可能为冻结期，可能之前就是冻结期了
        // 3状态为冻结状态，前天一定为1状态（并且这个状态只有一天）
        int[] dp = new int[4];
        // 初始化,持有股票
        dp[0] = -prices[0];
        // 递推
        for (int i = 1; i < length; i++) {
            // 一维优化，这里先保存旧的0和1的值，因为后面需要的是上一层也就是旧的值，当然也可以2行循环优化
            int oldZero = dp[0];
            int oldFirst = dp[1];
            // 之前状态可能为持有，可能为冻结，可能为持续卖出
            dp[0] = Math.max(dp[0], Math.max(dp[2] - prices[i], dp[3] - prices[i]));
            // 之前状态为持有
            dp[1] = oldZero + prices[i];
            // 之前的状态为持续卖出或者冻结，如果前状态为卖出，也就是1那么这里应该是3，只有2才可能这里为2
            dp[2] = Math.max(dp[2], dp[3]);
            // 之前状态为卖出状态
            dp[3] = oldFirst;
        }
        // 返回值，看1 2 3哪种状态收入多，0状态还未卖出，收益不完整
        return Math.max(dp[1], Math.max(dp[2], dp[3]));
    }
}

子序列问题

子序列（不连续）

300. 最长递增子序列

300. 最长递增子序列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int lengthOfLIS(int[] nums) {
        // 保存当前位置前面比自己大的数的个数，永远包括自己+1
        int[] dp = new int[nums.length];
        for (int i = 0; i < nums.length; i++) {
            int temp = 1;
            // 从头遍历也行，反正就是看比之前哪个大就在他的基础上+1，并不断比较前面所有数
            for (int j = i - 1; j >= 0; j--) {
                if (nums[i] > nums[j]) {
                    temp = Math.max(temp, dp[j] + 1);
                }
            }
            dp[i] = temp;
        }
        // 遍历dp看哪个最大
        int result = 1;
        for (int i : dp) {
            result = Math.max(result, i);
        }
        return result;
    }
}

1143. 最长公共子序列

1143. 最长公共子序列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        // 自己画画递归方程，发现也简单,可以循环数组优化
        int[][] dp = new int[text1.length() + 1][text2.length() + 1];
        // 最开始初始化为0即可，不用管，保存没一层对应text1的到当前字符的前面的字符串和text2对应的到当前字符串的最长的公共子序列，不需连续
        for (int i = 0; i < text1.length(); i++) {
            // 由于需要依靠前一个的值，倒序遍历
            for (int j = 0; j < text2.length(); j++) {
                // 两个字符相等就去看去掉这个字符的前面的字符串+上这个，就是+1大还是上一层结果大
                if (text1.charAt(i) == text2.charAt(j)) {
                    // j留多一个初始化和递推用，这里j+1才对得上
                    dp[i + 1][j + 1] = Math.max(dp[i][j] + 1, dp[i][j + 1]);
                } else {
                    // 不相等用前面的值和上面的值，看哪个大
                    dp[i + 1][j + 1] = Math.max(dp[i + 1][j], dp[i][j + 1]);
                }
            }
        }
        return dp[text1.length()][text2.length()];
    }
}

时间复杂度和空间复杂度比较高，优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        // 一维优化一下，也很简单
        int[] dp = new int[text2.length() + 1];
        for (int i = 1; i <= text1.length(); i++) {
            // 保存dp[i-1][j-1]其实，在一维最开始就是0下标
            int last = dp[0];

            for (int j = 1; j <= text2.length(); j++) {

                // 临时记录下上一层的
                int cur = dp[j];

                // 从1开始遍历的，好填表
                if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
                    // 前面一定是最优的，不用比较都可以
                    dp[j] = last + 1;
                } else {
                    // 上一层和前面一个看看哪个大，因为前面的本轮可能更新过，比上层大了就以新的为准
                    // dp[j] 相当于 dp[i - 1][j]
                    // dp[j - 1] 相当于 dp[i][j - 1]
                    dp[j] = Math.max(dp[j], dp[j - 1]);
                }

                // 放到last保存
                last = cur;
            }
        }

        return dp[text2.length()];
    }
}

1035. 不相交的线

1035. 不相交的线

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        // 跟前面一题很想，字符串换成这样而已，保证按顺序相同并且不能重复跟一个做比较就好
        int[] dp = new int[nums2.length + 1];

        for (int i = 1; i <= nums1.length; i++) {

            int last = dp[0];

            for (int j = 1; j <= nums2.length; j++) {

                int cur = dp[j];

                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[j] = last + 1;
                } else {
                    dp[j] = Math.max(dp[j], dp[j - 1]);
                }

                last = cur;

            }
        }

        return dp[nums2.length];

    }
}

子序列（连续）

674. 最长连续递增序列

674. 最长连续递增序列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int findLengthOfLCIS(int[] nums) {
        //贪心
        int result = 1,temp = 1,last = nums[0];
        for(int i = 1;i<nums.length;i++){
            if(nums[i]>last){
                result = Math.max(result,++temp);
            }else{
                temp = 1;
            }
            last = nums[i];
        }
        return result;
    }
}

动规就是大于前一个就前一个的dp+1，不然就是1，可以初始化全为1，也可以贪心保存最大，不然就是回去遍历一遍找到最大的，简单，不写了，看到这题肯定贪心的

718. 最长重复子数组

718. 最长重复子数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int findLength(int[] nums1, int[] nums2) {
        // 还是要有点贪心思想,不然要回头遍历了，这里相等就斜上角+1，不然就设置为0
        int result = 0;
        int[] dp = new int[nums2.length + 1];
        // 开始遍历填充dp
        for (int i = 0; i < nums1.length; i++) {
            // 需要借助[i-1][j-1]而已，就是dp[j-1]
            for (int j = nums2.length - 1; j >= 0; j--) {
                if (nums1[i] == nums2[j]) {
                    dp[j + 1] = dp[j] + 1;
                    result = Math.max(result, dp[j + 1]);
                } else {
                    dp[j + 1] = 0;
                }
            }
        }
        return result;
    }
}

编辑距离

392. 判断子序列

392. 判断子序列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public boolean isSubsequence(String s, String t) {
        // 双指针先写一次
        int len1 = s.length(), len2 = t.length();
        int i = 0, j = 0;
        while (i != len1 && j != len2) {
            // 相等共同移动，不然移动len2
            if (s.charAt(i) == t.charAt(j)) {
                i++;
                j++;
            } else {
                j++;
            }
        }
        return i == len1;
    }
}

动规

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public boolean isSubsequence(String s, String t) {
        // 这里也可以看作编辑距离问题，只有简单的删除，动态规划解决，其实思路跟前面的子序列很像，最长公共子序列
        //保存到i位置的第一个字符串和到j位置的第二个字符串的两个字符串的最大长度
        int[][] dp = new int[s.length() + 1][t.length() + 1];
        for (int i = 1; i <= s.length(); i++) {
            for (int j = 1; j <= t.length(); j++) {

                // 相等就是为两个都减一的结果+1就好
                if (s.charAt(i - 1) == t.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }

                // 不相等就是t减少一位但是i不变的值
                else {
                    dp[i][j] = dp[i][j - 1];
                }

            }
        }
        return s.length() == dp[s.length()][t.length()];
    }
}

583. 两个字符串的删除操作

583. 两个字符串的删除操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public int minDistance(String word1, String word2) {
        // 这就是找到两个公共最长的，然后分别删掉不是最长的就行，删除的个数就是步数
        int[][] dp = new int[word1.length() + 1][word2.length() + 1];

        for (int i = 1; i <= word1.length(); i++) {
            for (int j = 1; j <= word2.length(); j++) {

                // 相等就是都减少一个+1
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }

                // 不相等就看是第一个少一个大还是第二个少一个大
                else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }

        int max = dp[word1.length()][word2.length()];

        return word1.length() - max + word2.length() - max;
    }
}

上面取巧，下面思路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public int minDistance(String word1, String word2) {
        // dp保存下标到i和j的两个字符串到相等需要删除的最小的操作次数
        int[][] dp = new int[word1.length() + 1][word2.length() + 1];

        // 先看递归公式，需要初始化第一行和第一列，初始化为什么有点难想，一个为空，那么另一个就全删完那就是自己的长度
        for (int i = 0; i < word1.length() + 1; i++)
            dp[i][0] = i;
        for (int j = 0; j < word2.length() + 1; j++)
            dp[0][j] = j;

        for (int i = 1; i <= word1.length(); i++) {
            for (int j = 1; j <= word2.length(); j++) {

                // 相等就是不需要操作，就拿i-1和j-1下标
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1];
                }

                // 不相等就看删除左还是右的一个变为相等操作步数少
                else {
                    dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + 1;
                }
            }
        }

        return dp[word1.length()][word2.length()];
    }
}

72. 编辑距离

72. 编辑距离

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public int minDistance(String word1, String word2) {
        int[][] dp = new int[word1.length() + 1][word2.length() + 1];

        // 初始化，一个为空另一个不为空的最优情况就是有的全删了或者另一个全照着加，操作步数是一样的，这里也可以发现了，其实考虑删除就好了，删除也相当于另一个加一个，操作步数一样，可以不考虑增加了
        for (int i = 1; i <= word1.length(); i++) {
            dp[i][0] = i;
        }
        for (int j = 1; j <= word2.length(); j++) {
            dp[0][j] = j;
        }

        for (int i = 1; i <= word1.length(); i++) {
            for (int j = 1; j <= word2.length(); j++) {
                // 相等就不需要操作
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1];
                }
                // 不相等考虑删除、增加和替换,前面发现了删除和增加的操作步数都一样，考虑一个就好，替换的话其实就是替换一个字符就相等了，就是都减1的最少操作+1（替换当前位置其中一个字符就好）
                else {
                    dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + 1;
                    dp[i][j] = Math.min(dp[i][j], dp[i - 1][j - 1] + 1);
                }
            }
        }

        return dp[word1.length()][word2.length()];
    }
}

115. 不同的子序列

115. 不同的子序列

如果本题是求连续序列，就可以考虑KMP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public int numDistinct(String s, String t) {
        // 这里其实就是考虑编辑距离中的删除就好，这里不是连续，连续可以考虑KMP,以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]
        int[][] dp = new int[s.length() + 1][t.length() + 1];

        // 初始化，i不为0，但是j为0肯定是1，删除一个就可以得到了
        for (int i = 0; i <= s.length(); i++) {
            dp[i][0] = 1;
        }

        for (int i = 1; i <= s.length(); i++) {
            for (int j = 1; j <= t.length(); j++) {

                // 当前两个想等
                if (s.charAt(i - 1) == t.charAt(j - 1)) {
                    // 两个相等肯定都想到了dp[i-1][j-1]的结果就好，但还有一种情况是不用当前的也可以完成匹配的情况,s：bagg 和 t：bag ，s[3] 和
                    // t[2]是相同的，但是字符串s也可以不用s[3]来匹配，即用s[0]s[1]s[2]组成的bag
                    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
                }
                // 当前两个不等，删除当前i
                else {
                    dp[i][j] = dp[i - 1][j];
                }

            }
        }

        return dp[s.length()][t.length()];
    }
}

回文

647. 回文子串

647. 回文子串

动态规划写法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public int countSubstrings(String s) {
        // 这里跟平时的dp不太一样，平时更多是题目要求什么就去定义什么，但这里很明显发现递推关系很难求出来，这里就换了一种方式
        int result = 0;
        boolean[][] dp = new boolean[s.length()][s.length()];
        // 一开始初始化都为false就好，先看下面的递推公式决定遍历的顺序
        for (int i = s.length() - 1; i >= 0; i--) {
            // 夹起来的部分，不要遍历前面的，应该往后
            for (int j = i; j < s.length(); j++) {
                // 当前的两个下标夹起来的部分如果第一个和最后一个位置不相等就肯定不是了
                if (s.charAt(i) == s.charAt(j)) {
                    // 这里有三种情况，i==j；i和j相差1；相差大于1
                    if (i == j || j - i == 1 || dp[i + 1][j - 1]) {
                        result++;
                        dp[i][j] = true;
                        // 从下面这里可以发现最外层应该倒序遍历，需要知道下层的情况先
                    }
                }
            }
        }
        return result;
    }
}

双指针，时间复杂度和空间复杂度都更低

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int countSubstrings(String s) {
        //双指针写法,可以以一个作为中心，也可以以两个作为中心，中心扩散法，下面的情况可以一起写的，分开计算思路更加清晰
        int result = 0;
        //确定以一个作为中心和两个作为中心的所有可能性，n^2
        for(int i = 0;i<s.length();i++){
            result+=caculate(s,i,i);
            result+=caculate(s,i,i+1);
        }
        return result;
    }

    public int caculate(String s,int left,int right){
        int count = 0;
        while(left>=0&&right<s.length()&&s.charAt(left)==s.charAt(right)){
            count++;
            left--;
            right++;
        }
        return count;
    }
}

516. 最长回文子序列

516. 最长回文子序列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
    public int longestPalindromeSubseq(String s) {
        // i--j的最长子序列的长度
        int[][] dp = new int[s.length()][s.length()];
        // 初始化都为0就好,遍历根据递推公式需要知道下一层的先
        for (int i = s.length() - 1; i >= 0; i--) {
            for (int j = i; j < s.length(); j++) {
                // 相等
                if (s.charAt(i) == s.charAt(j)) {
                    if (i == j) {
                        dp[i][j] = 1;
                    } else if (j - i == 1) {
                        dp[i][j] = 2;
                    } else if (j - i > 1) {
                        dp[i][j] = dp[i + 1][j - 1] + 2;
                    }
                }
                // 不相等
                else {
                    // 两个靠在一起，删掉任何一个就行
                    if (j - i == 1) {
                        dp[i][j] = 1;
                    } else {
                        // 不靠在一起的话就看删哪个的结果更大
                        dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
                    }
                }
            }
        }

        return dp[0][s.length() - 1];
    }
}

优化版本，总结上面的进行优化，简化代码逻辑

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int longestPalindromeSubseq(String s) {
        // i--j的最长子序列的长度
        int[][] dp = new int[s.length() + 1][s.length() + 1];
        // 初始化都为0就好,遍历根据递推公式需要知道下一层的先
        for (int i = s.length() - 1; i >= 0; i--) {
            // 想等直接赋值就行,没有更多情况，相当于初始化
            dp[i][i] = 1;
            for (int j = i + 1; j < s.length(); j++) {
                // 相等
                if (s.charAt(i) == s.charAt(j)) {
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                }
                // 不相等
                else {
                    // 不靠在一起的话就看删哪个的结果更大
                    dp[i][j] = Math.max(dp[i][j], Math.max(dp[i + 1][j], dp[i][j - 1]));
                }
            }
        }

        return dp[0][s.length() - 1];
    }
}

数位dp

面试题 17.06. 2出现的次数

面试题 17.06. 2出现的次数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class Solution {

    // 不记忆化会超时
    int[][][] memory;

    public int numberOf2sInRange(int n) {
        // 要统计多少位，看gpt非常巧妙，直接转换为String去统计更快，避免计算了
        String s = String.valueOf(n);

        // 递归缓存，记忆化搜索,第一维度表示当前前面处理过的数量，第二维度表示当前出现的2的次数，最多就是全长度，不会更长的情况出现了，第三维度是是否可以任选,递归层数最多为数字的位数，自然count在递归中最大为数字的位数
        memory = new int[s.length()][s.length()][2];

        // 初始化
        for (int[][] nums : memory) {
            for (int[] init : nums) {
                Arrays.fill(init, -1);
            }
        }

        return dp(0, s, 0, false);
    }

    // solve已经处理过的位数,target为原本值，count为传递给下一轮的结果，isCanSelectedRandom是否可以任选
    public int dp(int solve, String target, int count, boolean isCanSelectedRandom) {
        if (solve == target.length()) {
            // 到最后一位，可以直接返回结果了
            return count;
        }

        // 看是否搜索过
        if (memory[solve][count][isCanSelectedRandom ? 1 : 0] != -1) {
            return memory[solve][count][isCanSelectedRandom ? 1 : 0];
        }

        int res = 0;

        // 上限，受是否任选的影响
        int limit = isCanSelectedRandom ? 9 : target.charAt(solve) - '0';

        for (int i = 0; i <= limit; i++) {
            int cnt = count + ((i == 2) ? 1 : 0);
            // 这层是任选的话这里以及下层一定可以仍选，但是这层不是的话就看选的是不是小于limit
            res += dp(solve + 1, target, cnt, isCanSelectedRandom || i < limit);
        }

        // 保存搜索过
        memory[solve][count][isCanSelectedRandom ? 1 : 0] = res;

        return res;
    }
}

233. 数字 1 的个数

233. 数字 1 的个数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution {

    // 记忆化
    int[][][] memory;

    public int countDigitOne(int n) {
        // 给虾皮虐完，力扣这里有
        String s = String.valueOf(n);

        memory = new int[s.length()][s.length()][2];
        for (int[][] init : memory) {
            for (int[] init1 : init) {
                Arrays.fill(init1, -1);
            }
        }

        return dp(s, 0, 0, false);

    }

    // deep为深度，也就是字符串长度
    public int dp(String s, int deep, int count, boolean isCanSelectRandom) {
        if (deep == s.length()) {
            return count;
        }

        if (memory[deep][count][isCanSelectRandom ? 1 : 0] != -1) {
            return memory[deep][count][isCanSelectRandom ? 1 : 0];
        }

        int limit = isCanSelectRandom ? 9 : s.charAt(deep) - '0';

        int ans = 0;
        for (int i = 0; i <= limit; i++) {
            ans += dp(s, deep + 1, count + (i == 1 ? 1 : 0), isCanSelectRandom || (i < limit));
        }

        memory[deep][count][isCanSelectRandom ? 1 : 0] = ans;

        return ans;
    }

}

图论

理论

基本理论

图论理论基础 | 代码随想录 (programmercarl.com)

任何两个节点都是可以到达的

无向图 连通图

有向图 强连通图

在无向图中的极大连通子图称之为该图的一个连通分量

在有向图中极大强连通子图称之为该图的强连通分量

构建

邻接矩阵 邻阶表

并查集理论

并查集常用来解决连通性问题，并查集主要有两个功能，第一个功能是将两个元素添加到一个集合中，第二个功能是判断两个元素在不在同一个集合。

并查集理论基础 | 代码随想录

1. 首先知道怎么表示并查集

这里用个一维数组表示就好，比如1->2，那么parent[2] = 1，表示2的parent也就是来者是1

所以说用一个一维数组表示就好，每个位置代表这个下标对应节点的parent

那怎么初始化呢？自己来自自己呗

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//并查集
class DisJoint{
    private int[] father;
    
    public DisJoint(int size){
        father = new int[size+1];
        init();
    }
    
    //初始化
    private void init(){
        for(int i = 1;i<father.length;i++){
            father[i] = i;
        }
    }
}

2. 之后就要知道并查集是怎么查找parent的

根据并查集的表示方式，怎么知道到根了呢，自然就是i = parent[i]，没得父亲找了，不然比如parent[1] = 2，那么就可以往2下标去找，parent[2] = 5，之后还要往5去找，parent[5] = 5，那么就到头了，可以找到1的root为5，也就是5->2->1是路径

那本次查找后就发现了，我要找5的root为1，2的root也为1，那是不是可以优化，也就是压缩路径呢，下次找5可以直接输出1即可，在递归中如果parent[i]!=i，就可以进行优化，是当然直接返回就好了

1
2
3
4
5
//find查找根
public int find(int u){
    //递归寻找同时压缩，father[u]更新为查找到的father，压缩路径
    return u == father[u] ? father[u] : (father[u] = find(father[u])); 
}

3. 下一步就是要知道怎么加入并查集了

要加入并查集有两个值一个为u，一个为v，其中u->v，那么并查集是表示可以连通的在一个集合中，如果这两个已经连通了就没必要加入了，不连通才需要去加入，说明有新连通，那么怎么判断是否在同一个集合，就找两个都root看是不是一样就好

1
2
3
4
5
6
7
8
9
10
//join加入并查集
public void join(int u, int v){
    //这里一定需要找到他们的父亲，父亲不同就让父亲相连，而不是u和v相连
    //所以需要find找到父亲
    u = find(u);
    v = find(v);
    if(u!=v){
        father[v] = u;
    }
}

4. 之后就是要判断两个节点是否是连通的

跟第三部分差不多，看两个节点的parent是否相等就行，上面的备注写的很清楚了，两个不同的时候加入并查集是让parent相连，而不是u和v相连，所以在join不能直接调用这个方法判断是否相连就让u和v相连

1
2
3
4
//判断两个节点是否连通
public boolean isSame(int u, int v){
    return find(u) == find(v);
}

整个类就是并查集的模板代码了，复制粘贴就好

下面看一下深搜和广搜在使用上的区别，广搜是用来解决最短路径问题的，深搜就没那么好用了，深搜就是回溯，一路到头再回来。下面用一道例题感受两者的区别就好

深搜

98. 所有可达路径

98. 所有可达路径 (kamacoder.com)

邻接矩阵写法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
import java.util.Scanner;
import java.util.ArrayList;
import java.util.List;


public class Main{
    public static void main (String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt(),m = scanner.nextInt();
        int[][] graph = new int[n+1][n+1];
        while(m!=0){
            graph[scanner.nextInt()][scanner.nextInt()] = 1;
            m--;
        }
        List<String>result= new ArrayList<>();
        List<Integer>temp = new ArrayList<>();
        boolean[] isVisited = new boolean[n+1];
        temp.add(1);
        isVisited[1] = true;
        backTracking(result,temp,n,graph,isVisited,1);
        
        if(result.isEmpty()){
            System.out.println("-1");
            return;
        }
        
        //打印
        for(int i = 0;i<result.size();i++){
            System.out.println(result.get(i));
        }
    }
    
    public static void backTracking(List<String>result,List<Integer>temp,int n,int[][] graph,boolean[] isVisited,int point) {
        //中止条件
        if(point==n){
            StringBuilder builder = new StringBuilder();
            for(int i = 0;i<temp.size();i++){
                builder.append(temp.get(i));
                builder.append(" ");
            }
            result.add(builder.toString().trim());
            return;
        }
        
        for(int i = 1;i<=n;i++){
            //防止循环,但题目说了不纯在环了其实
            if(!isVisited[i]&&graph[point][i]==1){
                isVisited[i] = true;
                temp.add(i);
                
                backTracking(result,temp,n,graph,isVisited,i);
                
                temp.remove(temp.size()-1);
                isVisited[i] = false;
            }
        }
    }
}

邻接表写法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
import java.util.*;


public class Main{
    public static void main (String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt(),m = scanner.nextInt();
        List<LinkedList<Integer>>graph = new ArrayList<>();
        for(int i = 0;i<=n;i++){
            graph.add(new LinkedList<>());
        }
        //输入
        while(m!=0){
            m--;
            graph.get(scanner.nextInt()).add(scanner.nextInt());
        }
        
        List<String>result = new ArrayList<>();
        List<Integer>path = new ArrayList<>();
        //不会存在回环，这里不考虑了
        path.add(1);
        backTracking(n,result,path,graph,1);
        
        
        //打印
        if(result.isEmpty()){
            System.out.println("-1");
            return;
        }
        for(String s:result){
            System.out.println(s);
        }
    }
    
    //这里是dfs，一些地方直接用dfs命名
    public static void backTracking(int n, List<String>result,List<Integer>path,List<LinkedList<Integer>>graph,int point){
        if(point==n){
            //保存结果
            StringBuilder builder = new StringBuilder();
            for(int i : path){
                builder.append(i);
                builder.append(" ");
            }
            result.add(builder.toString().trim());
            return;
        }
        
        for(int i:graph.get(point)){
            path.add(i);
            
            //递归
            backTracking(n,result,path,graph,i);
            
            //回溯
            path.remove(path.size()-1);
        }
    }
}

99. 岛屿数量

99. 岛屿数量 (kamacoder.com)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
import java.util.*;

public class Main{
    
    //上下左右
    public static int[][] dir = new int[][]{{1,0},{-1,0},{0,-1},{0,1}};
    
    public static void main (String[] args) {
        
        Scanner scanner = new Scanner(System.in);
        
        int n = scanner.nextInt(),m = scanner.nextInt();
        
        int[][] graph = new int[n][m];
        
        for(int i = 0;i<n;i++){
            for(int j = 0;j<m;j++){
                graph[i][j] = scanner.nextInt();
            }
        }
        
        int result = 0;
        
        
        boolean[][] isVisited = new boolean[n][m];
        for(int i = 0;i<n;i++){
            for(int j = 0;j<m;j++){
                //没访问过并且当前为岛
                if(!isVisited[i][j]&&graph[i][j]==1){
                    result++;
                    dfs(graph,isVisited,n,m,i,j);
                }
            }
        }
        
        System.out.println(result);
    }
    
    
    public static void dfs(int[][]graph,boolean[][] isVisited,int n,int m,int i,int j){
        //先标记为到过该地方
        isVisited[i][j] = true;
        for(int k = 0;k<4;k++){
            int nextI = i+dir[k][0];
            int nextJ = j+dir[k][1];
            //看下个位置是否越界和访问过并且是岛
            if(nextI>=0&&nextI<n&&nextJ>=0&&nextJ<m&&!isVisited[nextI][nextJ]&&graph[i][j]==1){
                //走到下个位置
                dfs(graph,isVisited,n,m,nextI,nextJ);
            }
        }
    }
}

广搜

99. 岛屿数量

99. 岛屿数量 (kamacoder.com)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
import java.util.*;

public class Main{
    
    //上下左右
    public static int[][] dir = new int[][]{{1,0},{-1,0},{0,-1},{0,1}};
    
    public static void main (String[] args) {
        
        Scanner scanner = new Scanner(System.in);
        
        int n = scanner.nextInt(),m = scanner.nextInt();
        
        int[][] graph = new int[n][m];
        
        for(int i = 0;i<n;i++){
            for(int j = 0;j<m;j++){
                graph[i][j] = scanner.nextInt();
            }
        }
        
        int result = 0;
        
        
        boolean[][] isVisited = new boolean[n][m];
        for(int i = 0;i<n;i++){
            for(int j = 0;j<m;j++){
                //没访问过并且当前为岛
                if(!isVisited[i][j]&&graph[i][j]==1){
                    result++;
                    bfs(graph,isVisited,i,j,n,m);
                }
            }
        }
        
        System.out.println(result);
    }
    
    
    
    public static void bfs(int[][] graph,boolean[][] isVisited,int i,int j,int n,int m){
        //这里用队列，用栈和队列都可以，只要保证每轮是一层一层往外扩展就好
        //标准库里面没有Pair，懒得自定义了，就用int[2]表示坐标吧
        Queue<int[]>queue = new LinkedList<>();
        //当前点一定存在的，是主函数放进来的
        //入队的时候就要加入访问过，而不是出队再做这件事，入队就说明被消耗掉了
        queue.offer(new int[]{i,j});
        isVisited[i][j] = true;
        //开始往外扩散直到扩散不了了
        while(!queue.isEmpty()){
            int[] cur = queue.poll();
            int curI = cur[0],curJ = cur[1];
            //开始看这个点的四周，没访问过入队，同样入队就设置访问过了
            for(int t = 0;t<4;t++){
                int nextI = curI + dir[t][0], nextJ = curJ + dir[t][1];
                //看是否符合要求
                if(nextI>=0 && nextI<n && nextJ>=0 && nextJ<m && !isVisited[nextI][nextJ]
                    && graph[nextI][nextJ]==1){
                        queue.offer(new int[]{nextI,nextJ});
                        isVisited[nextI][nextJ] = true;
                    }
            }
        }
    }
}

110. 字符串接龙

110. 字符串接龙

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
import java.util.*;

public class Main{
    public static void main (String[] args) {
        //输入
        Scanner scanner = new Scanner(System.in);
        
        int N = scanner.nextInt();
        
        //吞掉回车先
        scanner.nextLine();
        
        String[] words = scanner.nextLine().split(" ");
        
        List<String>dic = new ArrayList<>();
        for(int i = 0;i<N;i++){
            dic.add(scanner.nextLine());
        }
        
        //打印bfs返回的结果
        System.out.println(bfs(dic,words[0],words[1]));
    }
    
    public static int bfs(List<String> dic, String beginWord, String endWord){
        //保存每次变更一个字符串
        Queue<String>queue = new LinkedList<>();
        //HashMap保存遍历到的字符和路径长
        HashMap<String,Integer>map = new HashMap<>();
        //Set保存这个元素是否存在,字典放进去
        HashSet<String>set = new HashSet<>(dic);
        
        //进入先加入到map和队列
        queue.offer(beginWord);
        map.put(beginWord,1);
        
        //搜索
        while(!queue.isEmpty()){
            String curStr = queue.poll();
            int path = map.get(curStr);
            
            //从a-z去尝试修改每个位置，看是否能修改为字典中的，能就跑到字典中的
            //那个词并设置访问过
            for(int i = 0;i<curStr.length();i++){
                
                char[] chars = curStr.toCharArray();
                
                for(char c = 'a';c<='z';c++){
                    chars[i] = c;
                    String s = new String(chars);
                    //跟end相等，找到路径了，可以返回了
                    if(s.equals(endWord)){
                        return path+1;
                    }
                    //在set字典能找到一样的并没有访问过就直接访问，map存在说明有别的可能到这里，有路径到这就行
                    if(set.contains(s)&&!map.containsKey(s)){
                        //加入队列和map
                        queue.offer(s);
                        map.put(s,path+1);
                    }
                }
                
            }
        }
        
        //没找到路径
        return 0;
    }
}

题目

105. 有向图的完全可达性

105. 有向图的完全可达性

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
import java.util.*;

public class Main{
    public static void main (String[] args) {
        //这题深搜和广搜都是可以的，跟前面的路径数量有点区别就是这里不需要
        //知道所有的路径，只需要知道是否能走到这个点就行了，就不需要回溯
        
        Scanner scanner = new Scanner(System.in);
        
        int n = scanner.nextInt(), k = scanner.nextInt();
        
        //这里用邻接表
        List<List<Integer>>graph = new ArrayList<>();
        
        for(int i = 0;i<=n;i++){
            graph.add(new LinkedList<>());
        }
        
        //边
        for(int i = 0;i<k;i++){
            graph.get(scanner.nextInt()).add(scanner.nextInt());
        }
        
        
        boolean[] isVisited = new boolean[n+1];
        //深搜
        //dfs(graph,isVisited,1);
        //广搜
        bfs(graph,isVisited);
        for(int i = 1;i<=n;i++){
            if(!isVisited[i]){
                System.out.println(-1);
                return;
            }
        }
        System.out.println(1);
        
    }
    
    //深搜
    public static void dfs(List<List<Integer>>graph, boolean[] isVisited, int point){
        //访问过
        isVisited[point] = true;
        //当当前节点可以前往哪里
        for(int i : graph.get(point)){
            if(!isVisited[i]){
                dfs(graph,isVisited,i);
                //不需要回溯，到就不继续了，因为到的这个点在前面递归肯定处理过了
            }
        }
    }
    
    //广搜
    public static void bfs(List<List<Integer>>graph, boolean[] isVisited){
        Queue<Integer>queue = new LinkedList<>();
        queue.offer(1);
        isVisited[1] = true;
        while(!queue.isEmpty()){
            int point = queue.poll();
            for(int i : graph.get(point)){
                if(!isVisited[i]){
                    queue.offer(i);
                    isVisited[i] = true;
                }
            }
        }
    }
}

100. 岛屿的最大面积

100. 岛屿的最大面积 (kamacoder.com)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
import java.util.*;

public class Main{
    
    public static int[][] dir = new int[][]{{1,0},{-1,0},{0,-1},{0,1}};
    
    public static void main (String[] args) {
        
        
        Scanner scanner = new Scanner(System.in);
        
        int n = scanner.nextInt(),m = scanner.nextInt();
        
        int[][] graph = new int[n][m];
        
        for(int i = 0;i<n;i++){
            for(int j = 0;j<m;j++){
                graph[i][j] = scanner.nextInt();
            }
        }
        
        boolean[][] isVisited = new boolean[n][m];
        
        int result = 0;
        
        for(int i = 0;i<n;i++){
            for(int j = 0;j<m;j++){
                if(!isVisited[i][j]&&graph[i][j]==1){
                    result = Math.max(result,dfs(graph,isVisited,n,m,i,j));
                }
            }
        }
        
        System.out.println(result);
        
    }
    
    public static int dfs(int[][] graph,boolean[][] isVisited,int n,int m,int i,int j){
        isVisited[i][j] = true;
        int result = 1;
            
        //看邻近有有没有
        for(int k = 0;k<4;k++){
                
            int nextI = i+dir[k][0];
            int nextJ = j+dir[k][1];
                
            if(nextI>=0&&nextI<n&&nextJ>=0&&nextJ<m&&!isVisited[nextI][nextJ]&&graph[nextI][nextJ]==1){
                    
                result+=dfs(graph,isVisited,n,m,nextI,nextJ);
                    
            }
        }
            
        return result;
        
    }
}

101. 孤岛的总面积

101. 孤岛的总面积 (kamacoder.com)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
import java.util.*;

public class Main{
    
    public static int[][] dir = new int[][]{{1,0},{-1,0},{0,-1},{0,1}};
    
    public static void main (String[] args) {
        
        
        Scanner scanner = new Scanner(System.in);
        
        int n = scanner.nextInt(),m = scanner.nextInt();
        
        int[][] graph = new int[n][m];
        
        for(int i = 0;i<n;i++){
            for(int j = 0;j<m;j++){
                graph[i][j] = scanner.nextInt();
            }
        }
        
        int result = 0;
        
        //左右两边去找岛屿
        for(int i = 0;i<n;i++){
            if(graph[i][0]==1){
                dfs(graph,n,m,i,0);
            }
            if(graph[i][m-1]==1){
                dfs(graph,n,m,i,m-1);
            }
        }
        
        //上下两边去找岛屿
        for(int j = 0;j<m;j++){
            if(graph[0][j]==1){
                dfs(graph,n,m,0,j);
            }
            if(graph[n-1][j]==1){
                dfs(graph,n,m,n-1,j);
            }
        }
        
        //遍历整体，这里求面积也可以直接统计1的剩余数量就好
        for(int i = 0;i<n;i++){
            for(int j = 0;j<m;j++){
                if(graph[i][j]==1){
                    result += dfs(graph,n,m,i,j);
                }
            }
        }
        
        System.out.println(result);
        
    }
    
    // 很睿智的一个点是先遍历不是孤岛的部分，之后把他们全变为0，变成海洋，之后再遍历整个图看孤岛面积，
    // 这里用不上visited了，毕竟最后都处理为0了就不会进循环了
    public static int dfs(int[][] graph,int n,int m,int i,int j){
        
        int result = 1;
        
        //变为海洋
        graph[i][j] = 0;
            
        //看邻近有有没有
        for(int k = 0;k<4;k++){
                
            int nextI = i+dir[k][0];
            int nextJ = j+dir[k][1];
                
            if(nextI>=0&&nextI<n&&nextJ>=0&&nextJ<m&&graph[nextI][nextJ]==1){
                    
                result+=dfs(graph,n,m,nextI,nextJ);
                    
            }
        }
            
        return result;
        
    }
}

102. 沉没孤岛

102. 沉没孤岛 (kamacoder.com)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
import java.util.*;

public class Main{
    
    public static int[][] dir = new int[][]{{1,0},{-1,0},{0,-1},{0,1}};
    
    public static void main (String[] args) {
        
        
        Scanner scanner = new Scanner(System.in);
        
        int n = scanner.nextInt(),m = scanner.nextInt();
        
        int[][] graph = new int[n][m];
        //复制一份
        int[][] result = new int[n][m];
        
        for(int i = 0;i<n;i++){
            for(int j = 0;j<m;j++){
                graph[i][j] = scanner.nextInt();
                result[i][j] = graph[i][j];
            }
        }
        
        //左右两边去找岛屿
        for(int i = 0;i<n;i++){
            if(graph[i][0]==1){
                dfs(graph,n,m,i,0);
            }
            if(graph[i][m-1]==1){
                dfs(graph,n,m,i,m-1);
            }
        }
        
        //上下两边去找岛屿
        for(int j = 0;j<m;j++){
            if(graph[0][j]==1){
                dfs(graph,n,m,0,j);
            }
            if(graph[n-1][j]==1){
                dfs(graph,n,m,n-1,j);
            }
        }
        
        //遍历整体，这里求面积也可以直接统计1的剩余数量就好
        for(int i = 0;i<n;i++){
            for(int j = 0;j<m;j++){
                if(graph[i][j]==1){
                    //去掉孤岛
                    result[i][j] = 0;
                }
            }
        }
        
        //输出
        for(int i = 0;i<n;i++){
            for(int j = 0;j<m;j++){
                System.out.print(result[i][j]);
                System.out.print(" ");
            }
            System.out.println();
        }
    }
    
    // 很睿智的一个点是先遍历不是孤岛的部分，之后把他们全变为0，变成海洋，之后再遍历整个图看孤岛面积，
    // 这里用不上visited了，毕竟最后都处理为0了就不会进循环了
    public static int dfs(int[][] graph,int n,int m,int i,int j){
        
        int result = 1;
        
        //变为海洋
        graph[i][j] = 0;
            
        //看邻近有有没有
        for(int k = 0;k<4;k++){
                
            int nextI = i+dir[k][0];
            int nextJ = j+dir[k][1];
                
            if(nextI>=0&&nextI<n&&nextJ>=0&&nextJ<m&&graph[nextI][nextJ]==1){
                    
                result+=dfs(graph,n,m,nextI,nextJ);
                    
            }
        }
            
        return result;
        
    }
}

103. 水流问题

103. 水流问题 (kamacoder.com)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
//暴力每个点去深度搜索找到能到达边界的就是题目要求的，但是会超时
import java.util.*;

public class Main{
    public static void main (String[] args) {
        //这里用另外的方式，跟季风很像，就从四面八方从小到大往中间吹，都能吹到的地方就是满足条件的地方，反向思考
        Scanner scanner = new Scanner(System.in);    
        //输入
        int n = scanner.nextInt(),m = scanner.nextInt();
        int[][] graph = new int[n][m];
        for(int i = 0;i<n;i++){
            for(int j = 0;j<m;j++){
                graph[i][j] = scanner.nextInt();
            }
        }
        
        //两个boolean矩阵，分别表示从左和上吹过来的部分，和从右和下吹过来的部分，都吹到的部分就是需要的部分
        boolean[][] first = new boolean[n][m];
        boolean[][] second = new boolean[n][m];
        
        //从左和右深度搜索
        for(int i = 0;i<n;i++){
            //左
            dfs(graph,first,n,m,i,0,Integer.MIN_VALUE);
            //右
            dfs(graph,second,n,m,i,m-1,Integer.MIN_VALUE);
        }
        
        
        //从上和下深度搜索
        for(int i = 0;i<m;i++){
            //上
            dfs(graph,first,n,m,0,i,Integer.MIN_VALUE);
            //下
            dfs(graph,second,n,m,n-1,i,Integer.MIN_VALUE);
        }
        
        //保存结果
        List<List<Integer>>result = new ArrayList<>();
        for(int i = 0;i<n;i++){
            for(int j = 0;j<m;j++){
                if(first[i][j]&&second[i][j]){
                    result.add(Arrays.asList(i,j));
                }
            }
        }
        
        //打印
        for(List<Integer>list:result){
            System.out.print(list.get(0));
            System.out.print(" ");
            System.out.println(list.get(1));
        }
        
        
    }
    
    //深度搜索,pre为上次访问的点的数值
    public static void dfs(int[][] graph,boolean[][] isVisited,int n,int m,int i,int j,int pre){
        if(i>=0 && i<n && j>=0 && j<m && !isVisited[i][j] && pre<=graph[i][j]){
            isVisited[i][j] = true;
            
            //递归处理上下左右
            dfs(graph,isVisited,n,m,i+1,j,graph[i][j]);
            dfs(graph,isVisited,n,m,i-1,j,graph[i][j]);
            dfs(graph,isVisited,n,m,i,j-1,graph[i][j]);
            dfs(graph,isVisited,n,m,i,j+1,graph[i][j]);
        }
    }
}

104. 建造最大岛屿
104. 建造最大岛屿

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
import java.util.*;

public class Main{
    
    //当前这个岛屿的大小
    public static int size = 0;
    
    public static void main (String[] args) {
        //输入
        Scanner scanner = new Scanner(System.in);
        
        int m = scanner.nextInt(),n = scanner.nextInt();
        
        int[][] graph = new int[m][n];
        
        for(int i = 0;i<m;i++){
            for(int j = 0;j<n;j++){
                graph[i][j] = scanner.nextInt();
            }
        }
        
        //最大面积，在计算岛屿的时候要赋值到这里了，不填充的时候，也就是全满
        //的时候就是岛屿面积
        int max = 0;
        //当前要标记的岛屿数量
        int mark = 2;
        //统计不同编号的岛屿的面积
        HashMap<Integer,Integer>map = new HashMap<>();
        //是否访问过
        boolean[][] isVisited = new boolean[m][n];
        //填充和计算岛屿面积
        for(int i = 0;i<m;i++){
            for(int j = 0;j<n;j++){
                if(!isVisited[i][j]&&graph[i][j]==1){
                    size = 0;
                    dfs(graph,m,n,i,j,mark,isVisited);
                    map.put(mark,size);
                    mark++;
                    max = Math.max(max,size);
                }
            }
        }
        
        //填充为水的部分，看填充哪个位置跟他相邻的岛屿面积和最大
        for(int i = 0;i<m;i++){
            for(int j = 0;j<n;j++){
                if(graph[i][j]==0){
                    max = Math.max(max,caculateArea(graph,map,i,j,m,n));
                }
            }
        }
        
        //打印结果
        System.out.println(max);
    }
    
    //统计这个位置变为水后的最大面积
    public static int caculateArea(int[][] graph,HashMap<Integer,Integer>map,int i,int j,int m,int n){
        int result = 0;
        //统计过这个岛屿就不能统计了
        HashSet<Integer>set = new HashSet<>();
        for(int t = 0;t<4;t++){
            i+=dir[t][0];
            j+=dir[t][1];
            //看是否越界和是否是岛屿，不是岛屿不用处理了
            if(i<0||i>=m||j<0||j>=n||graph[i][j]==0){
                i-=dir[t][0];
                j-=dir[t][1];
                continue;
            }
            //是岛屿
            if(set.add(graph[i][j])){
                  result+=map.get(graph[i][j]);
            }
            i-=dir[t][0];
            j-=dir[t][1];
        }
        //加上当前位置
        result+=1;
        return result;
    }
    
    //将每个岛屿都标记为自己独特的数字，不能为0和1不然判断不出来，
    //然后哈希表记录一下不同岛屿标记的面积大小
    //这里可以根据mark的大小和1判断是否访问过的，可以不用visist数组判断是否访问过
    //这里还是先用vivit数组，用着顺手点
    public static int[][] dir = new int[][]{{-1,0},{1,0},{0,-1},{0,1}};
    public static void dfs(int[][] graph,int m,int n,int i,int j,int mark,boolean[][] isVisited){
        //越界或者访问过以及是水就不能操作
        if(i<0||i>=m||j<0||j>=n||isVisited[i][j]||graph[i][j]==0){
            return;
        }
        //增加面积
        size++;
        isVisited[i][j] = true;
        //修改标记
        graph[i][j] = mark;
        //递归四个方向
        for(int t = 0;t<4;t++){
            dfs(graph,m,n,i+dir[t][0],j+dir[t][1],mark,isVisited);
        }
     }
}

避免惯性思维引入

不是看到图就是广搜和深搜了

106. 岛屿的周长

106. 岛屿的周长

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
import java.util.*;

public class  Main{
    public static void main (String[] args) {
        //这里就一个岛屿，只需要统计岛屿格子的周长就好了，不需要深搜和广搜
        //只需要根据具体的规则来计算周长就好了
        
        Scanner scanner = new Scanner(System.in);
        
        int n = scanner.nextInt(), m = scanner.nextInt();
        
        int[][] graph = new int[n][m];
        
        for(int i = 0;i<n;i++){
            for(int j = 0;j<m;j++){
                graph[i][j] = scanner.nextInt();
            }
        }
        
        //看某个格子的四周如果是水或者贴到矩阵边界了就说明是一条边
        int result = 0;
        
        int[][] dir = new int[][]{{-1,0},{1,0},{0,-1},{0,1}};
        
        for(int i = 0;i<n;i++){
            for(int j = 0;j<m;j++){
                if(graph[i][j]==1){
                    //看上下左右是否是水或者越界就可以知道是否是边
                    for(int t = 0;t<4;t++){
                        int tempI = i + dir[t][0], tempJ = j + dir[t][1];
                        if(tempI<0||tempI>=n||tempJ<0||tempJ>=m||graph[tempI][tempJ]==0){
                            result++;
                        }
                    }
                }
            }
        }
        
        System.out.println(result);
    }
}

并查集题目

107. 寻找存在的路径

107. 寻找存在的路径

当然深搜也是能过的，但是并查集思想更快

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
import java.util.*;

public class Main{
    
    //标记是否能走到
    public static boolean isCanArrival = false;
    
    public static void main (String[] args) {
        
        //测试一下不用并查集能不能过
        
        Scanner scanner = new Scanner(System.in);
        
        int n = scanner.nextInt(), m = scanner.nextInt();
        
        //邻接表存储
        List<List<Integer>>graph = new ArrayList<>();
        for(int i = 0;i<=n;i++){
            graph.add(new LinkedList<>());
        }
        
        for(int i = 0;i<m;i++){
            int start = scanner.nextInt(), end = scanner.nextInt();
            graph.get(start).add(end);
            graph.get(end).add(start);
        }
        
        //起始点和终止点
        int begin = scanner.nextInt(), destination = scanner.nextInt();
        
        //看这个点是否走过，以防回头
        boolean[] isVisited = new boolean[n+1];
        
        //深搜
        dfs(graph,isVisited,begin,destination);
        
        System.out.println(isCanArrival?1:0);
        
    }
    
    public static void dfs(List<List<Integer>>graph, boolean[] isVisited, int point, int target){
        //可以到这里，可以回退了
        if(point==target){
            isCanArrival = true;
            return;
        }
        
        for(int i : graph.get(point)){
            if(!isVisited[i]){
                isVisited[i] = true;
                //不用回溯，走到这就走到了，因为走到的肯定处理过
                dfs(graph,isVisited,i,target);
            }
        }
    }
}

并查集解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
import java.util.*;

public class Main{
    
    public static void main (String[] args) {
        Scanner scanner = new Scanner(System.in);
        
        int n = scanner.nextInt(), m = scanner.nextInt();
        
        //新建并查集
        DisJoint disJoint = new DisJoint(n);
        
        //获取输入加入并查集
        for(int i = 0;i<m;i++){
            disJoint.join(scanner.nextInt(), scanner.nextInt());
        }
        
        //判断是否连通，就可以输出结果了
        if(disJoint.isSame(scanner.nextInt(), scanner.nextInt())){
            System.out.println(1);
        }else{
            System.out.println(0);
        }
    }
}

//并查集
class DisJoint{
    private int[] father;
    
    public DisJoint(int size){
        father = new int[size+1];
        init();
    }
    
    //初始化
    private void init(){
        for(int i = 1;i<father.length;i++){
            father[i] = i;
        }
    }
    
    //find查找根
    public int find(int u){
        //递归寻找同时压缩，father[u]更新为查找到的father，压缩路径
        return u == father[u] ? father[u] : (father[u] = find(father[u])); 
    }
    
    //join加入并查集
    public void join(int u, int v){
        //这里一定需要找到他们的父亲，父亲不同就让父亲相连，而不是u和v相连
        //所以需要find找到父亲
        u = find(u);
        v = find(v);
        if(u!=v){
            father[v] = u;
        }
    }
    
    //判断两个节点是否连通
    public boolean isSame(int u, int v){
        return find(u) == find(v);
    }
}

108. 冗余连接

108. 冗余连接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
import java.util.*;

public class Main{
    public static void main (String[] args) {
        //这里也是判断是否在一个集合中和是否会出现连通量，使用并查集更快
        Scanner scanner = new Scanner(System.in);
        
        int n = scanner.nextInt();
        
        DisJoint disJoint = new DisJoint(n);
        
        for(int i = 0;i<n;i++){
            int u = scanner.nextInt(), v = scanner.nextInt();
            if(disJoint.isSame(u, v)){
                System.out.printf("%d %d",u,v);
                return;
            }else{
                disJoint.join(u,v);
            }
        }
        
    }
}

//并查集
class DisJoint{
    private int[] father;
    
    public DisJoint(int size){
        father = new int[size+1];
        init();
    }
    
    //初始化
    private void init(){
        for(int i = 1;i<father.length;i++){
            father[i] = i;
        }
    }
    
    //寻找parent
    public int find(int u){
        return u == father[u] ? u : (father[u] = find(father[u])) ;
    }
    
    //加入并查集
    public void join(int u, int v){
        u = find(u);
        v = find(v);
        if(u!=v){
            father[v] = u;
        }
    }
    
    //判断是否连通
    public boolean isSame(int u, int v){
        return find(u) == find(v);
    }
}

109. 冗余连接II

109. 冗余连接II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
import java.util.*;

public class Main{
    
    //保存边信息，里面的0和1分别表示0->1下标的
    public static List<int[]>graph;
    //保存每个节点的入度数量，就是指向该节点的边的数量
    public static int[] edge;
    //并查集数组
    public static int[] father;
    
    public static void main (String[] args) {
        Scanner scanner = new Scanner(System.in);
        
        int n = scanner.nextInt();
        
        //初始化边集，输入保存
        graph = new ArrayList<>();
        //初始化入度数组
        edge = new int[n+1];
        for(int i = 0;i<n;i++){
            int begin = scanner.nextInt(), end = scanner.nextInt();
            graph.add(new int[]{begin, end});
            edge[end]++;
        }
        
        //根据题目介绍，n个节点应该n-1条边的，有条边多余的，每个节点的入度为1才行
        //那么入度为2的就不对，需要处理,只会有一个节点出现两个入度
        //这里保存删除掉哪条边，就是graph的下标
        //这里倒序遍历，需要输入标准输入的最后出现的一条边
        List<Integer>solve = new ArrayList<>();
        for(int i = n-1;i>=0;i--){
            if(edge[graph.get(i)[1]]==2){
                solve.add(i);
            }
        }
        
        //初始化并查集
        father = new int[n+1];
        
        //情况1和2，有度为2的，随便删除是一种情况和只能删除特定的
        //删除完判断满足树都条件就好了
        if(solve.size()>1){
            if(isTreeAfterDelete(solve.get(0))){
                System.out.printf("%d %d", graph.get(solve.get(0))[0],graph.get(solve.get(0))[1]);
            }else{
                System.out.printf("%d %d", graph.get(solve.get(1))[0],graph.get(solve.get(1))[1]);
            }
        }
        
        //情况3，没有度2为2的，说明有回环,会环解除一条边就行
        else{
            removeCircle();
        }
    }
    
    //初始化并查集
    public static void init(){
        for(int i = 1;i<father.length;i++){
            father[i] = i;
        }
    }
    
    //查找根
    public static int find(int u){
        return u == father[u] ? u : (father[u] = find(father[u]));
    }
    
    //加入并查集
    public static void join(int u, int v){
        u = find(u);
        v = find(v);
        if(u!=v){
            //不同集合
            father[v] = u;
        }
    }
    
    //判断两个节点是否是同个集合
    public static boolean isSame(int u, int v){
        return find(u) == find(v);
    }
    
    //判断删除这条边后是不是树
    public static boolean isTreeAfterDelete(int deleteEdge){
        //初始化并查集
        init();
        //遍历每条边
        for(int i = 0;i<graph.size();i++){
            //删除的边不管
            if(deleteEdge==i){
                continue;
            }
            //两个点的root相等说明形成回环了，因为0和1本来就相连了，两个点root还一样
            //肯定回环了
            if(isSame(graph.get(i)[0],graph.get(i)[1])){
                return false;
            }
            //加入并查集
            join(graph.get(i)[0],graph.get(i)[1]);
        }
        return true;
    }
    
    //解除回环
    public static void removeCircle(){
        //初始化并查集
        init();
        //遍历每条边
        for(int i = 0;i<graph.size();i++){
            //两个点的root相等说明形成回环了，因为0和1本来就相连了，两个点root还一样
            //肯定回环了，删除
            if(isSame(graph.get(i)[0],graph.get(i)[1])){
                System.out.printf("%d %d", graph.get(i)[0],graph.get(i)[1]);
                return;
            }else{
                //加入并查集
                join(graph.get(i)[0],graph.get(i)[1]);
            }
        }
    }
}

一些知识

Java常用容器

Java 提供了丰富的容器类（集合类）用于存储和操作数据。以下是一些常用的 Java 容器类，它们主要位于 java.util 包中，可以根据需要选择合适的容器：

List（列表）接口及其实现类

List 是一种有序的容器，允许重复元素。

  • ArrayList：

    • 基于动态数组实现，支持随机访问，适合频繁读取的场景。
    • 添加和删除操作的时间复杂度为 O(1)（在尾部添加），访问元素的时间复杂度为 O(1)。
    1
    List<String> list = new ArrayList<>();

  • LinkedList：

    • 基于双向链表实现，适合频繁插入和删除的场景。
    • 插入和删除的时间复杂度为 O(1)（在中间节点操作时），随机访问元素的时间复杂度为 O(n)。
    1
    List<String> list = new LinkedList<>();

  • Vector（较老，线程安全版的 ArrayList）：

    • 基于动态数组实现，线程安全。
    • 每次操作都同步，性能比 ArrayList 差，但适用于多线程环境。
    1
    List<String> list = new Vector<>();
  1. Set（集合）接口及其实现类

Set 是一种无序且不允许重复元素的容器。

  • HashSet：

    • 基于哈希表实现，允许 null 值，元素无序。
    • 添加、删除、查找的时间复杂度为 O(1)（假设哈希冲突少）。
    1
    Set<String> set = new HashSet<>();

  • LinkedHashSet：

    • 基于哈希表和链表实现，维护元素的插入顺序。
    • 添加、删除、查找的时间复杂度和 HashSet 一样为 O(1)，但会占用更多内存来维护顺序。
    1
    Set<String> set = new LinkedHashSet<>();

  • TreeSet：

    • 基于红黑树（自平衡二叉树）实现，元素是有序的。
    • 添加、删除、查找的时间复杂度为 O(log n)，适合需要排序的场景。
    1
    Set<String> set = new TreeSet<>();
  1. Map（映射）接口及其实现类

Map 是一种键值对（key-value）的映射结构，其中键不能重复。

  • HashMap：

    • 基于哈希表实现，允许 null 键和值，键值对无序。
    • 添加、删除、查找的时间复杂度为 O(1)（假设哈希冲突少）。
    1
    Map<String, Integer> map = new HashMap<>();

  • LinkedHashMap：

    • 基于哈希表和链表实现，维护键值对的插入顺序或访问顺序。
    • 性能类似于 HashMap，但可以保持插入顺序。
    1
    Map<String, Integer> map = new LinkedHashMap<>();

  • TreeMap：

    • 基于红黑树实现，键值对有序（根据键的自然顺序或自定义比较器）。
    • 添加、删除、查找的时间复杂度为 O(log n)。
    1
    Map<String, Integer> map = new TreeMap<>();

  • Hashtable（较老，线程安全版的 HashMap）：

    • 基于哈希表实现，线程安全，不允许 null 键和值。
    1
    Map<String, Integer> map = new Hashtable<>();
  1. Queue（队列）接口及其实现类

Queue 是一种先进先出（FIFO）的容器。

  • LinkedList（作为队列实现）：

    • 可以作为 Queue 实现，提供队列操作如 offer(), poll(), peek() 等。
    1
    Queue<String> queue = new LinkedList<>();

  • PriorityQueue：

    • 基于堆（优先队列）实现，元素根据自然顺序或自定义比较器排序。
    • 每次出队操作都是取优先级最高的元素。
    1
    Queue<Integer> queue = new PriorityQueue<>();
  1. Deque（双端队列）接口及其实现类

Deque 是一种双端队列，允许在两端进行插入和删除操作。

  • LinkedList（作为 Deque 实现）：

    • 可以作为 Deque 使用，提供双端队列操作。
    1
    Deque<String> deque = new LinkedList<>();

  • ArrayDeque：

    • 基于动态数组实现，作为双端队列的高效实现。
    • 比 LinkedList 更快，且不允许 null 元素。
    1
    Deque<String> deque = new ArrayDeque<>();
  1. Stack（栈）类

  • Stack

    （继承自 Vector，较老的栈实现）：

    • 线程安全，基于 Vector 实现，遵循后进先出（LIFO）原则。
    • 可以使用 push() 压栈，pop() 弹栈。
1
Stack<Integer> stack = new Stack<>();

注意：Stack 是较旧的类，通常推荐使用 Deque 来代替 Stack。

总结：

  • List：ArrayList, LinkedList, Vector。
  • Set：HashSet, LinkedHashSet, TreeSet。
  • Map：HashMap, LinkedHashMap, TreeMap, Hashtable。
  • Queue：LinkedList, PriorityQueue。
  • Deque：ArrayDeque, LinkedList。
  • Stack：Stack（推荐使用 Deque）。

选择容器类时，应该根据具体的使用场景选择合适的实现类，比如需要线程安全则使用 Vector 或 ConcurrentHashMap，需要排序则选择 TreeSet 或 TreeMap。

Java 中的容器类操作方法

Java 中的容器类提供了许多常用的方法来进行数据存储、检索、修改和操作。以下列举了各个常用容器类的一些常用方法：

  1. List 接口常用方法（ArrayList, LinkedList, Vector）

List 是一个有序集合，支持通过索引访问元素，允许重复元素。

1
List<String> list = new ArrayList<>();
  • add(E e)

    1
    2
    3
    4
    5

    ：在列表末尾添加元素。

    ```java
    list.add("Apple");
    

  • add(int index, E e)

    1
    2
    3
    4
    5

    ：在指定索引处添加元素。

    ```java
    list.add(1, "Banana");
    

  • get(int index)

    1
    2
    3
    4
    5

    ：获取指定索引处的元素。

    ```java
    String item = list.get(0);
    

  • set(int index, E e)

    1
    2
    3
    4
    5

    ：替换指定索引处的元素。

    ```java
    list.set(1, "Orange");
    

  • remove(int index)

    1
    2
    3
    4
    5

    ：移除指定索引处的元素。

    ```java
    list.remove(0);
    

  • remove(Object o)

    1
    2
    3
    4
    5

    ：移除列表中的某个元素（首次出现）。

    ```java
    list.remove("Apple");
    

  • size()

    1
    2
    3
    4
    5

    ：返回列表的大小。

    ```java
    int size = list.size();
    

  • contains(Object o)

    1
    2
    3
    4
    5

    ：判断列表中是否包含某个元素。

    ```java
    boolean hasApple = list.contains("Apple");
    

  • clear()

    1
    2
    3
    4
    5

    ：清空列表。

    ```java
    list.clear();
    

  • isEmpty()

    1
    2
    3
    4
    5

    ：判断列表是否为空。

    ```java
    boolean isEmpty = list.isEmpty();
  1. Set 接口常用方法（HashSet, LinkedHashSet, TreeSet）

Set 不允许重复元素，元素没有顺序（LinkedHashSet 和 TreeSet 有特定的顺序）。

1
Set<String> set = new HashSet<>();
  • add(E e)

    1
    2
    3
    4
    5

    ：添加元素到集合中，若元素已存在则不添加。

    ```java
    set.add("Apple");
    

  • remove(Object o)

    1
    2
    3
    4
    5

    ：从集合中移除元素。

    ```java
    set.remove("Apple");
    

  • contains(Object o)

    1
    2
    3
    4
    5

    ：判断集合中是否包含某个元素。

    ```java
    boolean hasApple = set.contains("Apple");
    

  • size()

    1
    2
    3
    4
    5

    ：返回集合的大小。

    ```java
    int size = set.size();
    

  • clear()

    1
    2
    3
    4
    5

    ：清空集合。

    ```java
    set.clear();
    

  • isEmpty()

    1
    2
    3
    4
    5

    ：判断集合是否为空。

    ```java
    boolean isEmpty = set.isEmpty();
  1. Map 接口常用方法（HashMap, LinkedHashMap, TreeMap, Hashtable）

Map 是键值对映射，键不能重复，值可以重复。

1
Map<String, Integer> map = new HashMap<>();
  • put(K key, V value)

    1
    2
    3
    4
    5

    ：向 Map中添加键值对。如果键已经存在，则覆盖旧的值。

    ```java
    map.put("Apple", 1);
    

  • get(Object key)

    1
    2
    3
    4
    5

    ：根据键获取对应的值。如果键不存在，则返回null

    ```java
    int count = map.get("Apple");
    

  • remove(Object key)

    1
    2
    3
    4
    5

    ：根据键移除键值对。

    ```java
    map.remove("Apple");
    

  • containsKey(Object key)

    1
    2
    3
    4
    5

    ：判断 Map中是否包含某个键。

    ```java
    boolean hasApple = map.containsKey("Apple");
    

  • containsValue(Object value)

    1
    2
    3
    4
    5

    ：判断 Map 中是否包含某个值。

    ```java
    boolean hasCount = map.containsValue(1);
    

  • size()

    1
    2
    3
    4
    5

    ：返回 Map的大小（键值对数量）。

    ```java
    int size = map.size();
    

  • clear()

    1
    2
    3
    4
    5

    ：清空Map

    ```java
    map.clear();
    

  • keySet()

    1
    2
    3
    4
    5

    ：返回 Map中所有键的集合。

    ```java
    Set<String> keys = map.keySet();
    

  • values()

    1
    2
    3
    4
    5

    ：返回 Map中所有值的集合。

    ```java
    Collection<Integer> values = map.values();
  1. Queue 接口常用方法（LinkedList, PriorityQueue）

Queue 是先进先出（FIFO）的数据结构，通常用于队列操作。

1
Queue<String> queue = new LinkedList<>();
  • offer(E e)

    1
    2
    3
    4
    5
    6
    7

    ：添加元素到队列的末尾，返回 true

    （如果队列有容量限制且插入失败则返回 false)

    ```java
    queue.offer("Apple");
    

  • poll()

    1
    2
    3
    4
    5

    ：从队列的头部移除并返回元素。如果队列为空，返回 null

    ```java
    String item = queue.poll();
    

  • peek()

    1
    2
    3
    4
    5

    ：获取队列头部的元素，但不移除。如果队列为空，返回null

    ```java
    String head = queue.peek();
    

  • size()

    1
    2
    3
    4
    5

    ：返回队列的大小。

    ```java
    int size = queue.size();
    

  • isEmpty()

    1
    2
    3
    4
    5

    ：判断队列是否为空。

    ```java
    boolean isEmpty = queue.isEmpty();
  1. Deque 接口常用方法（ArrayDeque, LinkedList）

Deque 是双端队列，可以在两端插入和删除元素。

1
Deque<String> deque = new ArrayDeque<>();
  • offerFirst(E e)

    1
    2
    3
    4
    5

    ：在队列的头部插入元素。

    ```java
    deque.offerFirst("Apple");
    

  • offerLast(E e)

    1
    2
    3
    4
    5

    ：在队列的尾部插入元素。

    ```java
    deque.offerLast("Banana");
    

  • pollFirst()

    1
    2
    3
    4
    5

    ：从队列头部移除并返回元素。

    ```java
    String first = deque.pollFirst();
    

  • pollLast()

    1
    2
    3
    4
    5

    ：从队列尾部移除并返回元素。

    ```java
    String last = deque.pollLast();
    

  • peekFirst()

    1
    2
    3
    4
    5

    ：获取队列头部的元素，但不移除。

    ```java
    String first = deque.peekFirst();
    

  • peekLast()

    1
    2
    3
    4
    5

    ：获取队列尾部的元素，但不移除。

    ```java
    String last = deque.peekLast();
  1. Stack 类常用方法

Stack 是后进先出（LIFO）的数据结构，继承自 Vector。

1
Stack<String> stack = new Stack<>();
  • push(E e)

    1
    2
    3
    4
    5

    ：将元素压入栈顶。

    ```java
    stack.push("Apple");
    

  • pop()

    1
    2
    3
    4
    5

    ：移除并返回栈顶元素。

    ```java
    String item = stack.pop();
    

  • peek()

    1
    2
    3
    4
    5

    ：返回栈顶元素但不移除。

    ```java
    String top = stack.peek();
    

  • isEmpty()

    1
    2
    3
    4
    5

    ：判断栈是否为空。

    ```java
    boolean isEmpty = stack.isEmpty();

总结

  • List：add, get, set, remove, size, contains, clear 等。
  • Set：add, remove, contains, size, clear 等。
  • Map：put, get, remove, containsKey, containsValue, keySet, values 等。
  • Queue：offer, poll, peek, size, isEmpty 等。
  • Deque：offerFirst, offerLast, pollFirst, pollLast, peekFirst, peekLast 等。
  • Stack：push, pop, peek, isEmpty 等。

每个容器类的方法都是围绕数据的存储、检索和修改来设计的。选择合适的方法和容器，能够提高代码的效率和可读性。

Java 基础——Scanner 类_java scanner-CSDN博客

Java的输入和输出_java输入语句怎么写-CSDN博客

image-20241016114305978

面试真题

小米2023秋季

151. 手机流畅运行的秘密

151. 手机流畅运行的秘密 (kamacoder.com)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
import java.util.*;

public class Main{
    public static void main(String[] args){
        Scanner scanner = new Scanner(System.in);
        
        String input = scanner.next();
        
        String[] s1 = input.split(",");
        
        int[][] task = new int[s1.length][2];
        for(int i = 0;i<task.length;i++){
            String[] temp = s1[i].split(":");
            task[i][0] = Integer.valueOf(temp[0]);
            task[i][1] = Integer.valueOf(temp[1]);
        }
        
        //优先处理差值大的，尽量剩多电量给下面的任务
        Arrays.sort(task,(a,b)->{
            return Math.abs(b[1]-b[0])-Math.abs(a[1]-a[0]);
        });

        
        int result = 0,balance = 0;
        for(int i =0;i<task.length;i++){
            //还可以不断取任务耗电量和初始化最大值进行剩下操作
            
            if(balance>=task[i][1]){
                //够
                balance-=task[i][0];
            }else{
                //不够
                int temp = task[i][1]-balance;
                result+=temp;
                balance = balance+temp-task[i][0];
            }
        }
        
        if(result>4800){
            System.out.println(-1);
        }else{
            System.out.println(result);
        }
    }
}

152. 小米手机通信校准

152. 小米手机通信校准 (kamacoder.com)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int freq = scanner.nextInt();
        List<String> list = new ArrayList<>();
        while (scanner.hasNext()) {
            list.add(scanner.next());
        }
        int[][] losses = new int[list.size()][2];
        for (int i = 0; i < list.size(); i++) {
            String[] temp = list.get(i).split(":");
            losses[i][0] = Integer.valueOf(temp[0]);
            losses[i][1] = Integer.valueOf(temp[1]);
        }

        // 用于保存最接近的索引
        int closestIndex = 0;
        int left = 0, right = losses.length - 1;
        double result = 0;

        // 二分查找，也可以不二分，一个个去找就行
        while (left <= right) {
            int mid = left + (right - left) / 2;

            if (Math.abs(losses[mid][0] - freq) < Math.abs(losses[closestIndex][0] - freq)) {
                closestIndex = mid;
            }

            if (losses[mid][0] > freq) {
                right = mid - 1;
            } else if (losses[mid][0] < freq) {
                left = mid + 1;
            } else {
                // 找到了完全匹配的情况，直接返回
                System.out.printf("%.1f", (double) losses[mid][1]);
                return;
            }
        }

        // 检查 left 和 right 是否越界
        if (left < losses.length) {
            if (Math.abs(losses[left][0] - freq) < Math.abs(losses[closestIndex][0] - freq)) {
                closestIndex = left;
            }
        }
        if (right >= 0) {
            if (Math.abs(losses[right][0] - freq) < Math.abs(losses[closestIndex][0] - freq)) {
                closestIndex = right;
            }
        }

        // 如果 high 和 left 距离相等，则取平均值
        if (left < losses.length && right >= 0 && Math.abs(losses[left][0] - freq) == Math.abs(losses[right][0] - freq)) {
            result = (losses[left][1] + losses[right][1]) / 2.0;
        } else {
            result = losses[closestIndex][1];
        }

        System.out.printf("%.1f", result);
    }
}

美团2023秋季

128. 小美的排列询问

https://kamacoder.com/problempage.php?pid=1204

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import java.util.*;

public class Main{
    public static void main(String[] args){
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int[] list = new int[n];
        for(int i = 0;i<n;i++){
            list[i] = scanner.nextInt();
        }
        
        int first = scanner.nextInt();
        int second = scanner.nextInt();
        
        for(int i = 1;i<n;i++){
            if((list[i-1]==first&&list[i]==second)||(list[i-1]==second&&list[i]==first)){
                System.out.println("Yes");
                return;
            }
        }
        
        System.out.println("No");
    }
}

129. 小美走公路

129. 小美走公路 (kamacoder.com)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);

        int n = scanner.nextInt(); // 数组长度
        int[] need = new int[n + 1]; // 定义数组来保存消耗量
        
        
        //总和
        long sum = 0L;
        for (int i = 1; i <= n; i++) {
            need[i] = scanner.nextInt();
            sum+=need[i];
        }

        int x = scanner.nextInt(); 
        int y = scanner.nextInt();

        if(x==y){
            System.out.println(0);
            return;
        }
        
        if(x>y){
            //起点大于终点转为小于，最后求一半，总和减掉就是另一半的走法
            int temp = x;
            x = y;
            y = temp;
        }
        
        long result = 0L;
        while(x<y){
            result+=need[x];
            x++;
        }
        
        System.out.println(Math.min(result,sum-result));
    }
}

130. 小美的蛋糕切割

130. 小美的蛋糕切割 (kamacoder.com)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
import java.util.*;

public class Main{
    public static void main (String[] args) {
        Scanner scanner = new Scanner(System.in);
        int x = scanner.nextInt(),y =scanner.nextInt();
        
        //需要考虑横切和竖切
        int[] rowSum = new int[x];
        int[] columnSum = new int[y];
        
        //输入后直接把每列的和保存
        int[] sum = new int[y];
        for(int i = 0;i<x;i++){
            for(int j = 0;j<y;j++){
                int temp = scanner.nextInt();
                rowSum[i]+=temp;
                columnSum[j]+=temp;
            }
        }
        
        //保存0到j列的块的和,0到i行的和
        int total = 0;
        int[] rowDp = new int[x];
        int[] columnDp =new int[y];
        total+=rowSum[0];
        rowDp[0] = rowSum[0];
        columnDp[0] = columnSum[0];
        for(int i = 1;i<x;i++){
            rowDp[i] = rowDp[i-1]+rowSum[i];
            total+=rowSum[i];
        }
        for(int j = 1;j<y;j++){
            columnDp[j] = columnDp[j-1]+columnSum[j];
        }
        
        //横切
        int result = Integer.MAX_VALUE;
        for(int i = 0;i<x;i++){
            result = Math.min(result,Math.abs(total-rowDp[i]-rowDp[i]));
        }
        
        //竖切
        for(int j = 0;j<y;j++){
            result = Math.min(result,Math.abs(total-columnDp[j]-columnDp[j]));
        }    
                
        System.out.println(result);
    }
}

131. 小美的字符串变换

131. 小美的字符串变换 (kamacoder.com)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
import java.util.*;

public class Main{
    public static void main (String[] args) {
        
         int result = Integer.MAX_VALUE;
        
        Scanner scanner = new Scanner(System.in);
        //获取输入
        int n = scanner.nextInt();
        String s = scanner.next();
        char[] chars = s.toCharArray();
        
        
        int len = chars.length;
        //构建不同形状，查看多少个岛然后找最小值返回
        for(int row = 1;row<=len;row++){
            //列
            int column = len/row;
            //是矩形才去操作
            if(row*column==len){
                //这里row和column分别代表行数和列数
                char[][] graph = new char[row][column];
                
                
                int flag = 0;
                
                //填充进去
                for(int i = 0;i<row;i++){
                    for(int j = 0;j<column;j++){
                       graph[i][j] = chars[flag++]; 
                    }
                }
                
                result = Math.min(result,solve(graph,row,column));
            }
        }
        
        System.out.println(result);
    
    }
    
    
    //找有多少个相连的岛屿
    public static int solve(char[][]graph,int n,int m){
        int result = 0;
        
        boolean[][] isVisited = new boolean[n][m];
        
        for(int i = 0;i<n;i++){
            for(int j = 0;j<m;j++){
                //看是否访问过
                if(!isVisited[i][j]){
                    //多一块
                    result++;
                    dfs(graph,isVisited,n,m,i,j);
                }
            }
        }
        
        return result;
    }
    
    //四个方向 
    public static int[][] dir = new int[][]{{1,0},{-1,0},{0,-1},{0,1}};
    public static void dfs(char[][] graph,boolean[][] isVisited,int n,int m,int i,int j){
        isVisited[i][j] = true;
        
        for(int k = 0;k<4;k++){
            int nextI = i+dir[k][0];
            int nextJ = j+dir[k][1];
            
            
            //看是否越界和访问过并且和当前字符一样
            if(nextI>=0&&nextJ>=0&&nextI<n&&nextJ<m&&!isVisited[nextI][nextJ]
                &&graph[i][j]==graph[nextI][nextJ]){
                    
                    dfs(graph,isVisited,n,m,nextI,nextJ);
                    
                }
        }
        
    }
}

132. 小美的树上染色

132. 小美的树上染色 (kamacoder.com)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
import java.util.*;

public class Main{
    public static void main (String[] args) {
        Scanner scanner = new Scanner(System.in);
        int count = scanner.nextInt();
        
        //邻接表
        List<List<Integer>>graph = new ArrayList<>();
        for(int i = 0;i<=count;i++){
            graph.add(new ArrayList<>());
        }
        
        //每个节点的值
        int[] points = new int[count+1];
        
        for(int i = 1;i<=count;i++){
            points[i] = scanner.nextInt();
        }
        
        while(scanner.hasNextInt()){
            //双向边
            int u = scanner.nextInt();
            int v = scanner.nextInt();
            graph.get(u).add(v);
            graph.get(v).add(u);
        }
        
        int[] result = new int[]{0};
        //某个节点是否访问过
        boolean[] isVisited = new boolean[count+1];
        //从节点1开始递归
        dfs(result,isVisited,points,graph,1,-1);
        System.out.println(result[0]);
    }
    
    //u当前节点，v邻居节点，parent为当前节点的上一个parent，这里不能回到上一个，只能跟邻居去涂，并且涂过也不能涂了
    public static void dfs(int[] result,boolean[] isVisited,int[]points,List<List<Integer>>graph,int u,int parent){
        //遍历所有邻居
        for(int v:graph.get(u)){
            //两个节点，跟另外一个不一样才能再进递归，避免回到父节点
            if(v!=parent){
                //先看孩子能不能涂，如果每层涂自己和孩子递归不好做，因为涂完这两个，孩子就不能涂了，要涂孩子的孩子难表示
                dfs(result,isVisited,points,graph,v,u);
                
                if(!isVisited[v]&&!isVisited[u]){
                         //看两数和是不是完全平方数
                int sqrt = (int)Math.sqrt(points[v]*points[u]);
                if(sqrt*sqrt==points[v]*points[u]){
                        //没访问过才进递归
                        isVisited[v] = true;
                        isVisited[u] = true;
                        result[0]+=2;
                    }
                }
            }
        }
    }
}

字节跳动2023秋季

147. 三珠互斥

147. 三珠互斥 (kamacoder.com)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
import java.util.*;

public class Main{
    public static void main (String[] args) {
        Scanner scanner = new Scanner(System.in);
        
        int count = scanner.nextInt();
        
        int[] dis = new int[3]; 
        
        while(count--!=0){
            
            int n = scanner.nextInt();
            int k = scanner.nextInt();
            int a1 = scanner.nextInt();
            int a2 = scanner.nextInt();
            int a3 = scanner.nextInt();
            
            // k*3超出距离可以不用判断了
            if((long)(k*3)>n){
                System.out.println(-1);
                continue;
            }
            
            //接下来分别看三个珠子之间的距离，最短距离
            dis[0] = Math.min(Math.abs(a1-a2),n-Math.abs(a1-a2));
            dis[1] = Math.min(Math.abs(a1-a3),n-Math.abs(a1-a3));
            dis[2] = Math.min(Math.abs(a2-a3),n-Math.abs(a2-a3));
            
            //可以手动取得最小的两个值就可以不排序了
            Arrays.sort(dis);
            
            
            int result = 0;
            if(dis[0]<k){
                result+=(k-dis[0]);
            }
            if(dis[1]<k){
                result+=(k-dis[1]);
            }
            
            System.out.println(result);
            
        }
    }
}

148. 扑克牌同花顺

148. 扑克牌同花顺 (kamacoder.com)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
import java.util.*;

public class Main{
    public static void main (String[] args) {
        
        Scanner scanner = new Scanner(System.in);
        
        
        int count = scanner.nextInt();
        
        HashMap<Integer,Integer>mapS = new HashMap<>();
        HashMap<Integer,Integer>mapH = new HashMap<>();
        HashMap<Integer,Integer>mapD = new HashMap<>();
        HashMap<Integer,Integer>mapC = new HashMap<>();
        
        for(int i = 0;i<count;i++){
            int num = scanner.nextInt();
            int size = scanner.nextInt();
            String type = scanner.next();
            
            
            if(type.equals("S")){
                mapS.put(num,mapS.getOrDefault(num,0)+size);
            }else if(type.equals("H")){
                mapH.put(num,mapH.getOrDefault(num,0)+size);
            }else if(type.equals("D")){
                mapD.put(num,mapD.getOrDefault(num,0)+size);
            }else{
                mapC.put(num,mapC.getOrDefault(num,0)+size);
            }
            
        }
        
        //分别处理四个花色
        long res = 0L;
        res+=solve(mapS);
        res+=solve(mapH);
        res+=solve(mapD);
        res+=solve(mapC);

        
        System.out.println(res);
    }
    
    
    public static long solve(HashMap<Integer,Integer>map){
        long result = 0L;
        
        //看连着的四个花色是否够用就是最大的可能
        for(int i1 : map.keySet()){
            int i2 = i1+1;
            int i3 = i1+2;
            int i4 = i1+3;
            int i5 = i1+4;
            
            //看是不是都有，这里i1还要在判断，可能被前面消耗了
            int minCount = map.getOrDefault(i1,0);
            minCount = Math.min(minCount,map.getOrDefault(i2,0));
            minCount = Math.min(minCount,map.getOrDefault(i3,0));
            minCount = Math.min(minCount,map.getOrDefault(i4,0));
            minCount = Math.min(minCount,map.getOrDefault(i5,0));
            
            //不为0就说明有组合
            if(minCount!=0){
                result+=minCount;
                //更新map
                map.put(i1,map.get(i1)-minCount);
                map.put(i2,map.get(i2)-minCount);
                map.put(i3,map.get(i3)-minCount);
                map.put(i4,map.get(i4)-minCount);
                map.put(i5,map.get(i5)-minCount);
            }
        }
        
        return result;
    }
}

149. 好数组

149. 好数组 (kamacoder.com)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
import java.util.*;

public class Main{
    public static void main (String[] args) {
    
        //获取输入    
        Scanner scanner = new Scanner(System.in);
    
        int count = scanner.nextInt();
    
        int[] ints = new int[count];
        for(int i = 0;i<count;i++){
            ints[i] = scanner.nextInt();
        }
        
        //结论就是换成中位数，想到一半了，没想到怎么去保留最小的那个是哪个，其实就是删第一个或者最后一个位置就行
        Arrays.sort(ints);
        
        //排序后第一个和最后一个相等就是全一样了，随便选一个删除就好
        if(ints[0]==ints[count-1]){
            System.out.println(1);
            return;
        }
        
        int[] ints1 = new int[count-1];
        int[] ints2 = new int[count-1];
        
        //删除第一个
        for(int i = 1;i<count;i++){
            ints1[i-1] = ints[i];
        }
        
        //删除最后一个
        for(int i = 0;i<count-1;i++){
            ints2[i] = ints[i];
        }
        
        System.out.println(Math.min(solve(ints1),solve(ints2)));
    }
    
    
    public static long solve(int[] ints){
        //求排序后的数组全部换成中位数需要的操作数量
        long result = 0L;
        int len = ints.length;
        //看是奇数个还是偶数个
        //奇数，就一个中位数
        if(len%2!=0){
            int mid = ints[len/2];
            for(int i = 0;i<len;i++){
                result+= Math.abs(ints[i]-mid);
            }
        }else{
            //偶数，两个中位数
            int mid1 = ints[len/2];
            int mid2 = ints[len/2-1];
            long res1 = 0L,res2 = 0L;
            for(int i = 0;i<len;i++){
                res1+=Math.abs(ints[i]-mid1);
                res2+=Math.abs(ints[i]-mid2);
            }
            result = Math.min(res1,res2);
        }
        return result;
    }
}

150. 极长连续段的权值

150. 极长连续段的权值 (kamacoder.com)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
import java.util.*;

public class Main{
    public static void main (String[] args) {
        
        Scanner scanner = new Scanner(System.in);
        
        int n = scanner.nextInt();
        
        String s = scanner.next();
        
        long result = 1L;
        
        
        long temp = 1L;
        //初始就一个，优化过的，没优化的就是都是0，没优化超时
        
        // 发现dp可以优化到只用一个temp表示本层就行
        // for(int i = n-1;i>=0;i--){
        //     for(int j = i;j<n;j++){
        //         //两个相等就是只有一个字符
        //         if(i==j){
        //             temp = 1;
        //         }else{
        //             //跟前一个不相同+1
        //             if(s.charAt(j)!=s.charAt(j-1)){
        //                 temp+=1;
        //             }
        //         }
        //         result+=temp;
        //     }
        // }
        
        
        // 动规还能再优化呢，可以发现求和部分可以直接基于上层了，二维还是会超时，好变态
        for(int i = 1;i<n;i++){
            //加上这一列最下面只有一个的时候
            temp = temp+1;
            if(s.charAt(i)!=s.charAt(i-1)){
                //不一样的话，列对应的每个行的值都要加上1，就刚好i个
                temp+=i;
            }
            result+=temp;
        }
        
        
        System.out.println(result);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public void reorderList(ListNode head) {
        int count = 0;
        ListNode node = head;
        while(node!=null){
            count++;
            node = node.next;
        }
        //偶数个
        if(count%2==0){
            count/=2;
        }
        //奇数个
        else{
            count = count/2+1;
        }
        node = head;
        while((count--)!=0){
            node = node.next;
        }
        //下一个需要翻转
        ListNode next = node.next;
        node.next = null;
        next = reverse(next);
        //开始组装
        node = head;
        while(node!=null){
            ListNode temp = node.next;
            temp.next = next;
            ListNode temp2 = next.next;
            next.next = temp;
            next = temp2;
            node = temp;
        }
    }

    //翻转
    public ListNode reverse(ListNode head){
        ListNode node = head,last = null;
        while(node!=null){
            ListNode next = node.next;
            node.next = last;
            last = node;
            node = next;
        }
        return last;
    }
}